第5章　「BOARD;GAME 負荷領域のデジャヴ」 by ni-ni (72)

5.1　始まりと終わりのプロローグ

あらすじ

自己紹介

みなさんおはようございます、ni-niです。カタログの方でも自己紹介はしたのですが、本記事でも一応しときますね。HNはni-niです。他の部員からは「にぃに〜」みたいな感じで呼ばれています。ちなみにこのHNは友人がつけてくれたものです。割と呼びやすいしセンスを感じます(僕個人の感想)。

HNの話はここまでにして、自己紹介を始めます。この部に入部したのは中2の夏頃(現在高1)で，他の部員に比べて結構遅れていますw。今まではUnity使ってゲーム作ったりしてました。ただ、なんにせよ素材がなくて作れるものは制限されるんですけどね。BGMやSE、キャラクターの3Dモデルなど諸々が用意できないので今まで作ってきたのは相当シンプルなものばかりです。最近は(ようやく)HTMLやらCSSの勉強始めました。初心者すぎてまだまだなので精進していきたいです(汗)

他には、人工知能(AI)に興味があるので線形代数を勉強し始めました。正直に申して、勉強する時間が少ない……。ちょっと悩んでるんですが、中学の頃は自主的に何かをしていたわけではなかったので、色々なことに手をつけすぎで右往左往しています(うおーっさおーっ)。さらにさらに、高1になって受験のことを意識し始めたため受験に向けた勉強も少しずつ始めています。もうお分かりでしょうか？完全に破綻しています……。ま、まぁこの辺りのお話はhideo54と被っているので僕もhideoさんの記事を参考に、頑張っていきたいと思います。

概略

さて、いい加減僕の自己紹介にも飽きてきたでしょう。この記事の概略を説明していきたいと思います。先ほどの自己紹介にも書いたように、僕は人工知能に興味があります。そこで、とりあえずゲームAIを作ってみようと思い立ったわけですね。ですが、未だに線形代数や統計学の知識が不足していて、機械学習や深層学習といった今流行りの人工知能は到底作れません。そこで、「学習しない」人工知能を作ってみることにしました。その題材として、ボードゲームを僕は選択しました。モンハンやストリートファイターのキャラクター、モンスターのAIでもよかったのですが、やはり素材がないとどうしようもないので。ボードゲームなら特に素材は必要ないので(デザイン等にこだわるなら別)

じゃ、本編行ってみよー

5.2　盤上彷徨のランデヴー

さて、先ほど僕はボードゲームを作ったと書きましたね。では、どんなボードゲームなのか？実はボードゲームAIについて調べると一番例として挙げられているのはオセロなのです。ですが、僕の謎のこだわりが発動してオセロは作りませんでした。代わりに「立体5目並べ」を作りました。

立体5目並べとは？

みなさん5目並べはご存知でしょうか？2人用のボードゲームで、先攻が黒、後攻が白の石を打っていきます。どちらかが縦横斜め1列に5個連続して石を置けたら勝利です。詳しくはググってください(丸投げ)

さて、その5目並べに「立体」とついています。どういう意味でしょうか？

5目並べは平面状で縦横斜めのどれかに5つ連続で石を並べるゲームです。しかし、立体5目並べは立体になったので、縦横だけでなく、高さが加わります。つまり、高さ1列もありということです。この辺りは言葉で説明してもわかりにくいと思いうので実際のプレイ画面貼ります。

ここように、勝つための石の並べ方が格段に増えます。様々な角度から状況を見て次の手を考える必要がありますね。

どうでしょうか？立体5目並べについて分かっていただけましたか？次は実際にどのようなAIを作るか、どうやって動くかを書いていきます。

5.3　創意限界のドクマ

ここでは実際にどのようにAIが動いているかを書いていきたいと思います。既出の内容が多い記事となりますが、ご了承ください。

概要

まずAIにどのような挙動が必要か、列挙してみましょう。

• 盤面の状況(どこにどちら側の石があるか)を判断
• どこに石を置くのが良いか探索
• 石を置く

こんな感じですね。1つ目と3つ目は特に書くことがないと思います。黒の石があれば1、白の石があれば-1、石がなければ0と数値で置き換えれば盤面判断は容易です。石を置くのも最適な手を導きさえすればそこに石をセットするだけです。正直、2つ目がAIの全てって感じです。

今回は探索と評価についてお話をしていきたいと思います。

探索する

ではまず探索から。探索というのは言葉の通り、最適な手を探索することです。今回はα-β法という手法をとりました。α-β法とは探索アルゴリズムの1つです。これと似た探索アルゴリズムにミニマックス法というものがあります。α-β法とはミニマックス法を拡張したものです。簡単に言うとミニマックス法の進化版です。強いのです。

ミニマックス法について

α-β法はミニマックス法を拡張したものなので、ミニマックス法のお話から。そもそもミニマックス法は「相手が常に自分にとって不利な手を打ってくる」という前提のもとに成り立っています。なので、相手が最適(ここでいう最適とは自分にとってもっとも不利であること)な手以外を打ってくることは考慮に入れていません。それでは、ここからは図を交えて解説をしていきます。下の図は「ゲーム木」と呼ばれるもので、これを使って最適な解を探索します。(ゲーム木1)

ちなみに、1つ1つの丸は「ノード」と呼ばれます。そして「CノードはAノードの子ノードである」と言います。1つ下の階層のノードを子ノードと呼びます。もちろん、1つ上のノードは親ノードと呼びます。

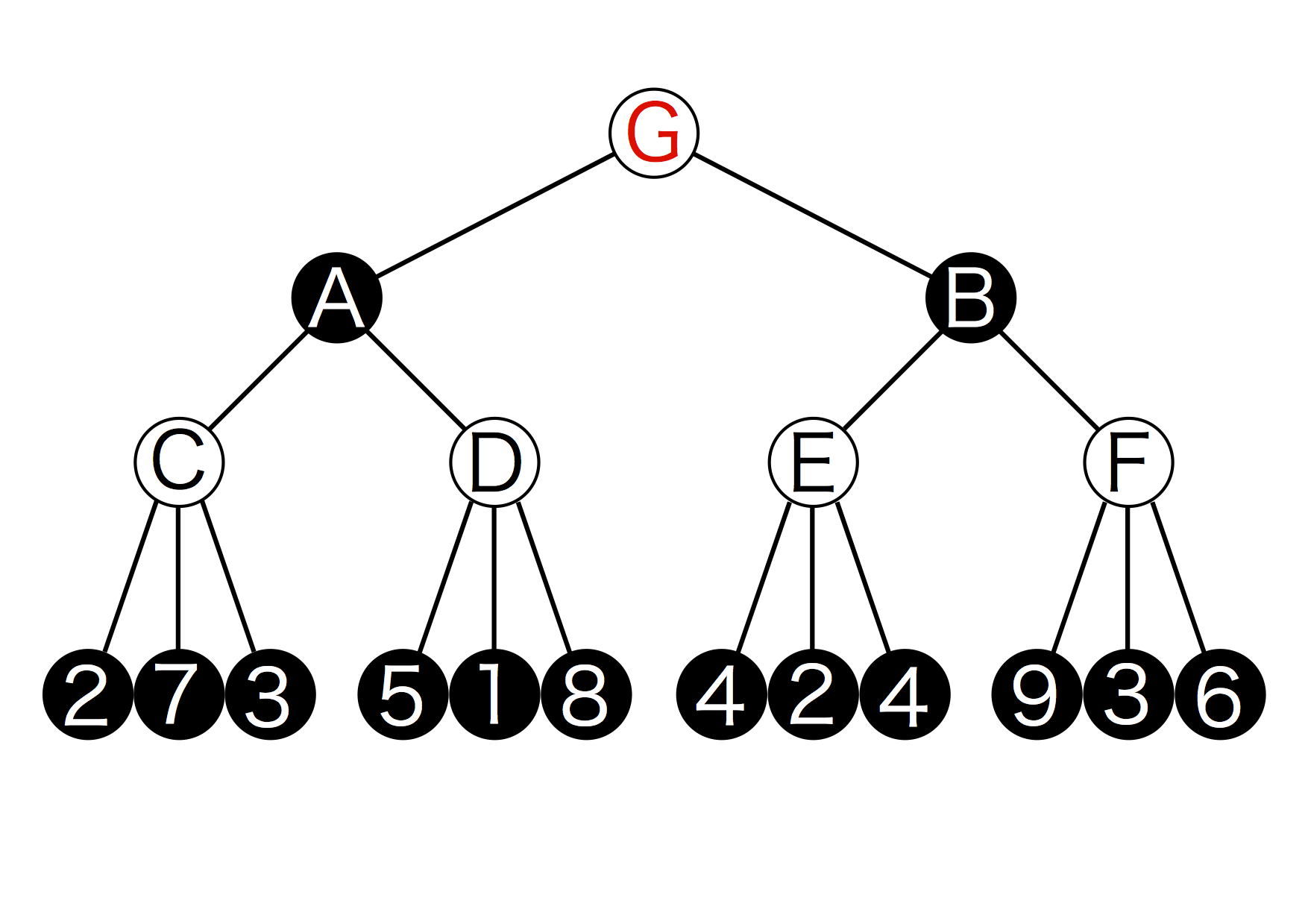
図5.1: ゲーム木1

この図は3手先まで読んだ場合のゲーム木です。仮にAIを白、プレイヤー(AIからすると敵)を黒とします。現在の盤面はGで次に手を打つのがAI(白)だとします。そしてこの図はGの状態から打てる手が2パターン存在することを表すとします。それぞれの手を打った時にに現れる盤面はAとBです。さらに、 Aから打てる手は2つ存在しそれぞれCとDの盤面が現れます。このように打つ手によってどんどん枝分かれしていきます。これがゲーム木です。この図において求めたい(探索したい)手はGの状態から打つ手となります。この場合は2択ですが、実際はもっと選択肢があります。今回は3手先まで読むとしているので、それ以上は枝分かれしていません。

さて、一番下に数字が並んでいますね。これは評価値と呼ばれるもので盤面における有利さ(不利さ)を表した数値です。今回は数字が大きいほどAIにとって有利であるとします。そうすると一見「9」が数字の中で最大なのでもっとも有利な手だと思えます。ですが、先ほど書いたように「相手が常に自分にとって不利な手を打ってくる」前提で探索するアルゴリズムなので、そうやすやすと相手が「9」を選ばしてくれません。ではどのように探索していくのでしょうか？

まず、G→A→Cの順で探索を行います。つまりAになるような手を打った後にCになるような手を打った場合を仮定します。Cから手を打った時、現れる盤面の点数は2と7と3ですね。Cから手を打つのは白のAIなので、自分にとって最も有利な手を打つために一番点数の高い7を選択します。(ゲーム木2)

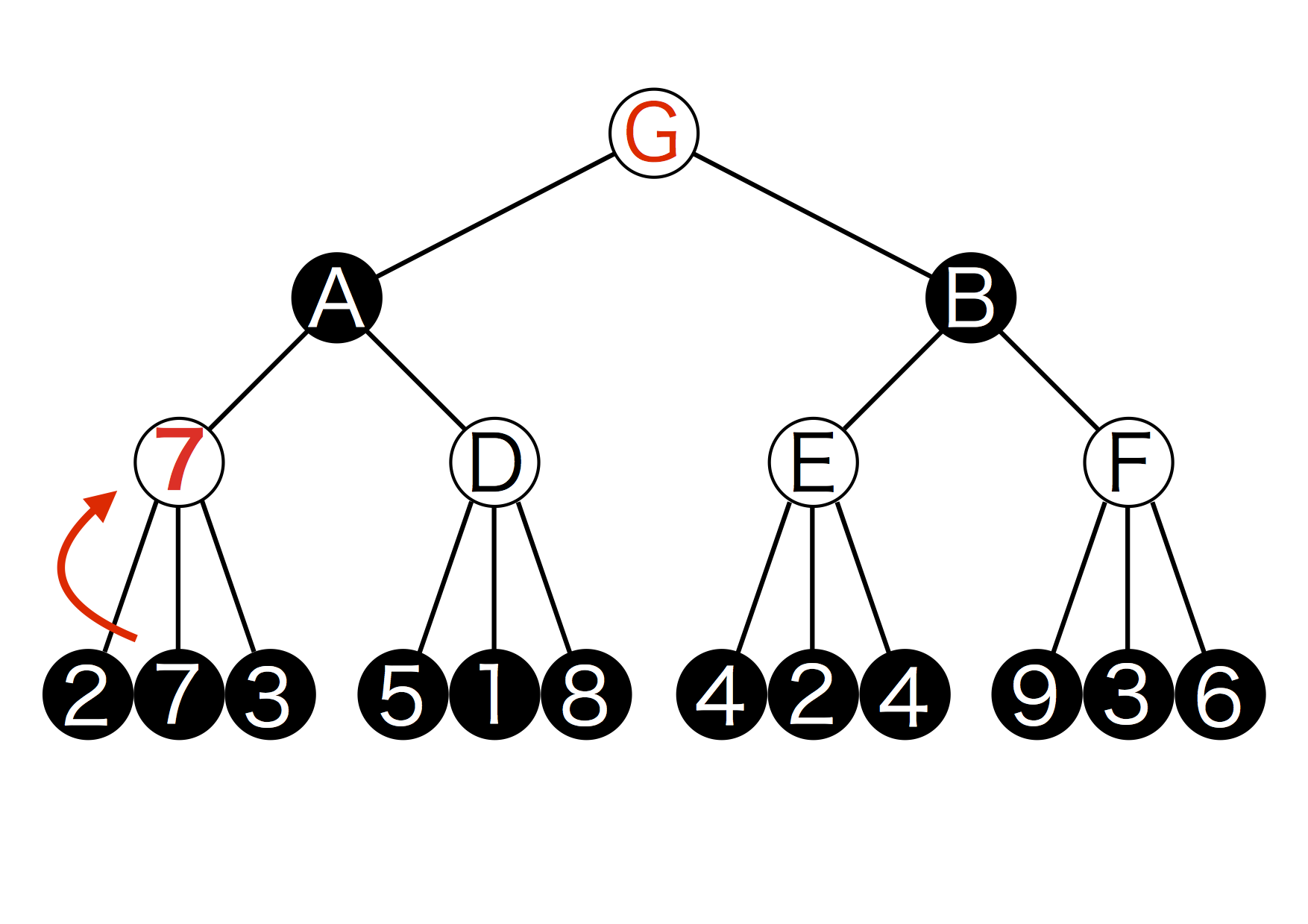
図5.2: ゲーム木2

これでCから打つ最適の手は7を選択することだとわかりました。この操作をDとEとFについても行います。ここで、Eから打てる手のうち、最大のものは4で2通りあります。今は左の4を選択しますがどちらでも良いです。(ゲーム木3)

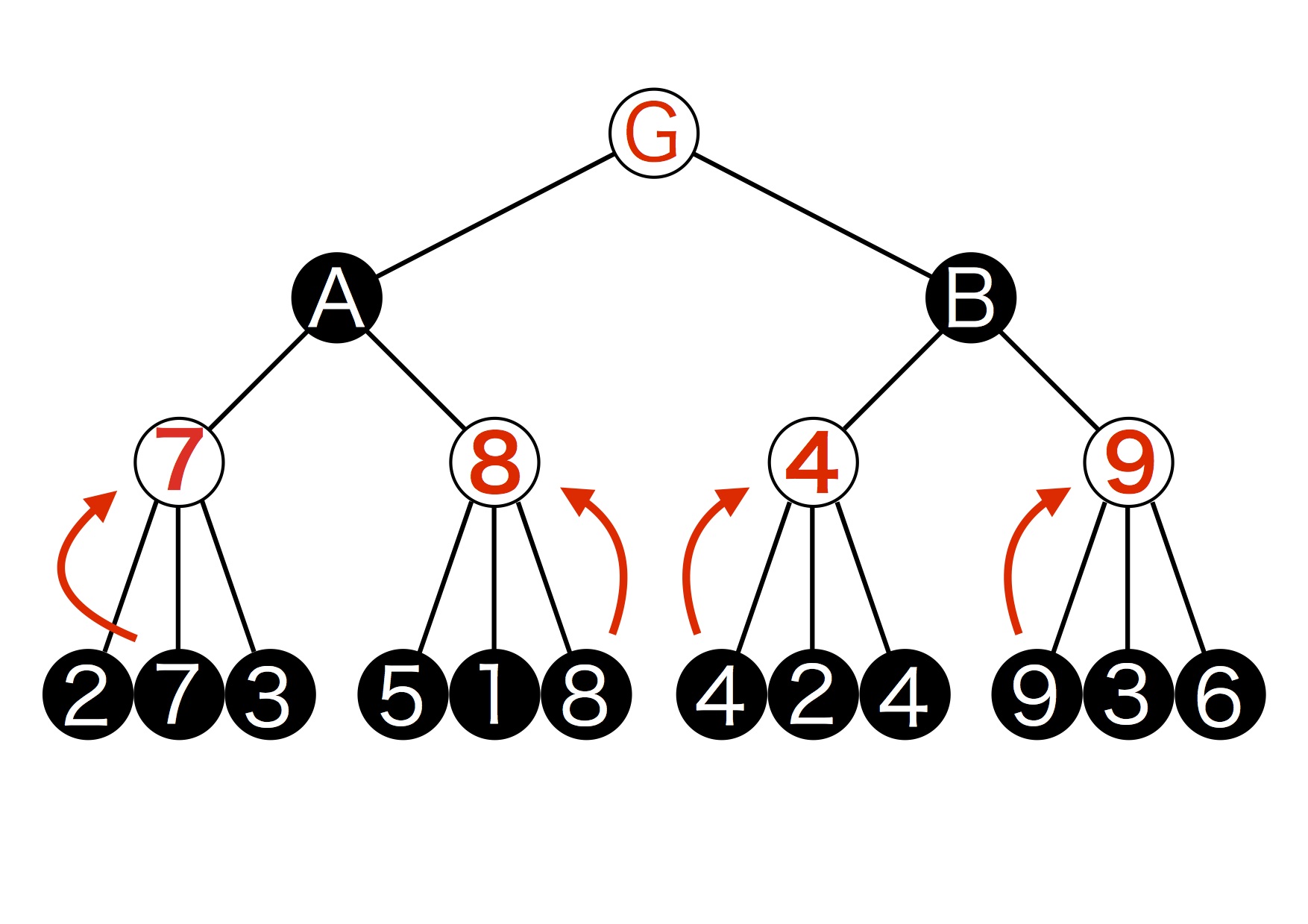
図5.3: ゲーム木3

ここで探索が1段階終了しました。次にAとBから打てる手を調べていきます。この時注意しなければならないのはAとBから手を打つのは敵なのでAIにとって最も不利な手、すなわち最も数値が小さくなる手を選択してきます(これはミニマックス法が成り立っている前提からくる)。なので、例えばAから手を打つ敵は7と8のうち小さいほうの7を選択します。(ゲーム木4)

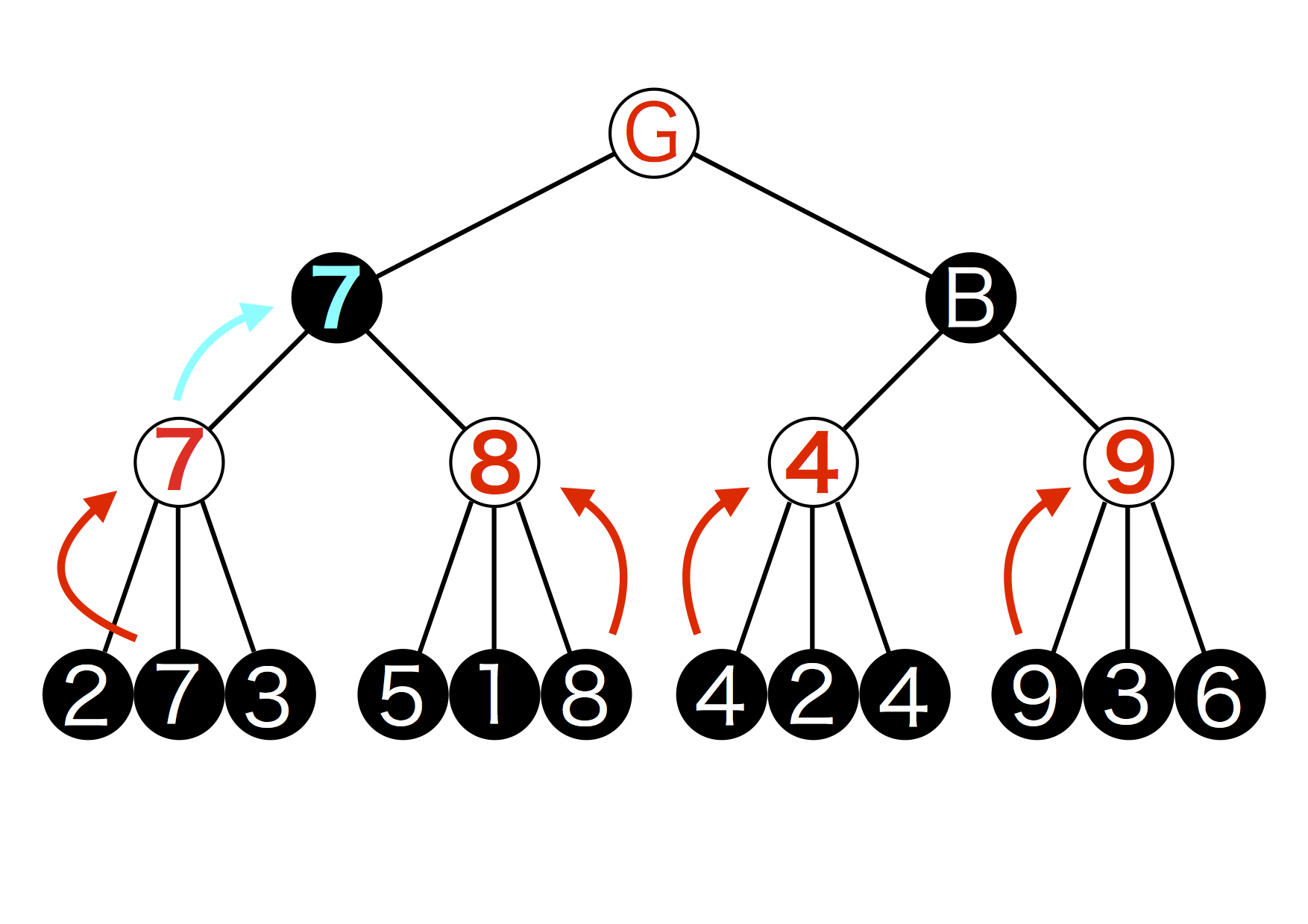
図5.4: ゲーム木4

Bにもこの操作を行います。4と9のうちAIにって不利な方である4が選ばれますね。(ゲーム木5)

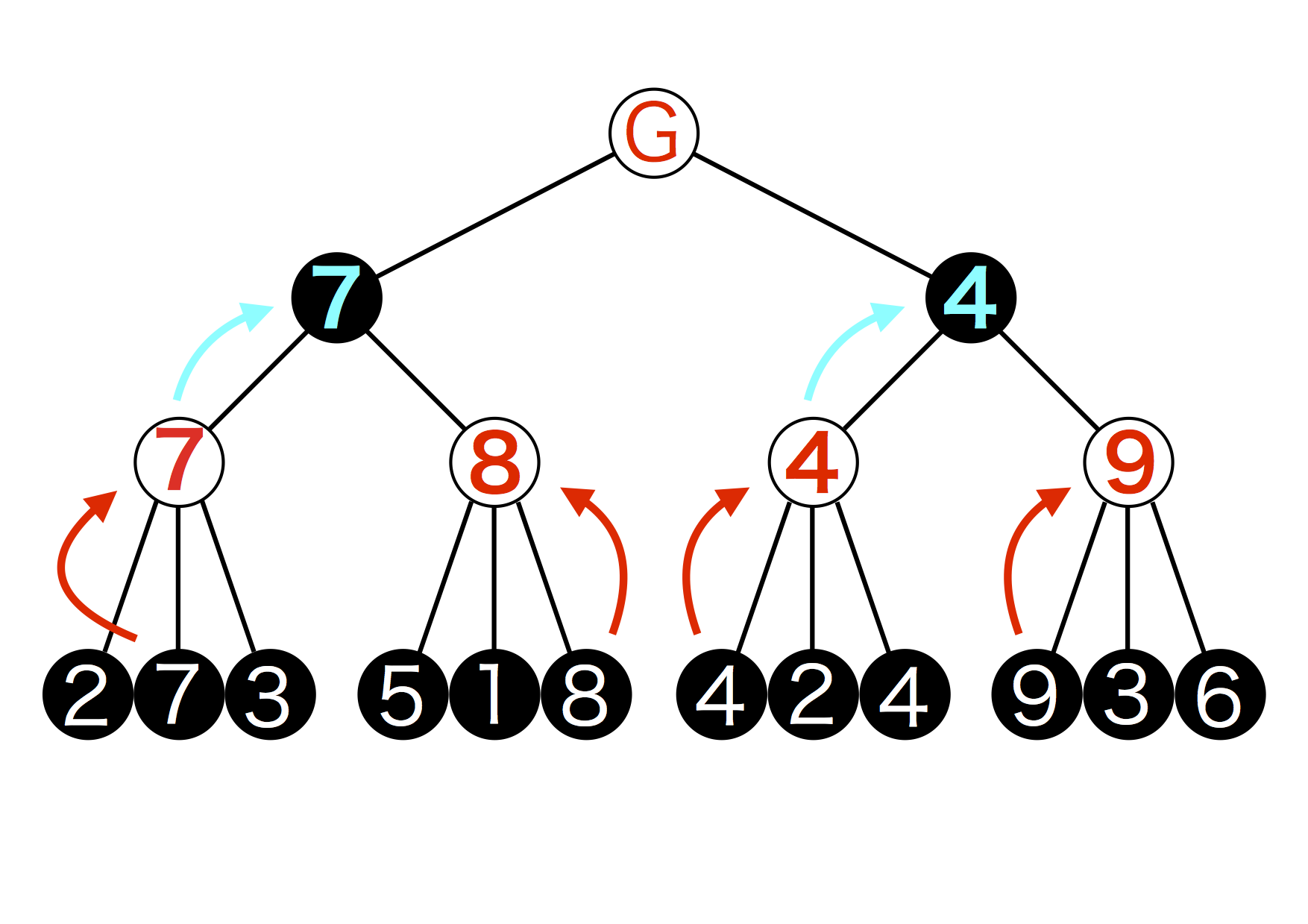
図5.5: ゲーム木5

さぁもうすぐ求めたかったGからの最適な手が導けます。もうおわかりかと思いますが、Gから手を打つのはAIなので最も有利になる、つまり数値が最大となる手を選びます。7と4を比較すると7の方が大きいですね。これでGからの最適な手は7だとわかりました。(ゲーム木6)

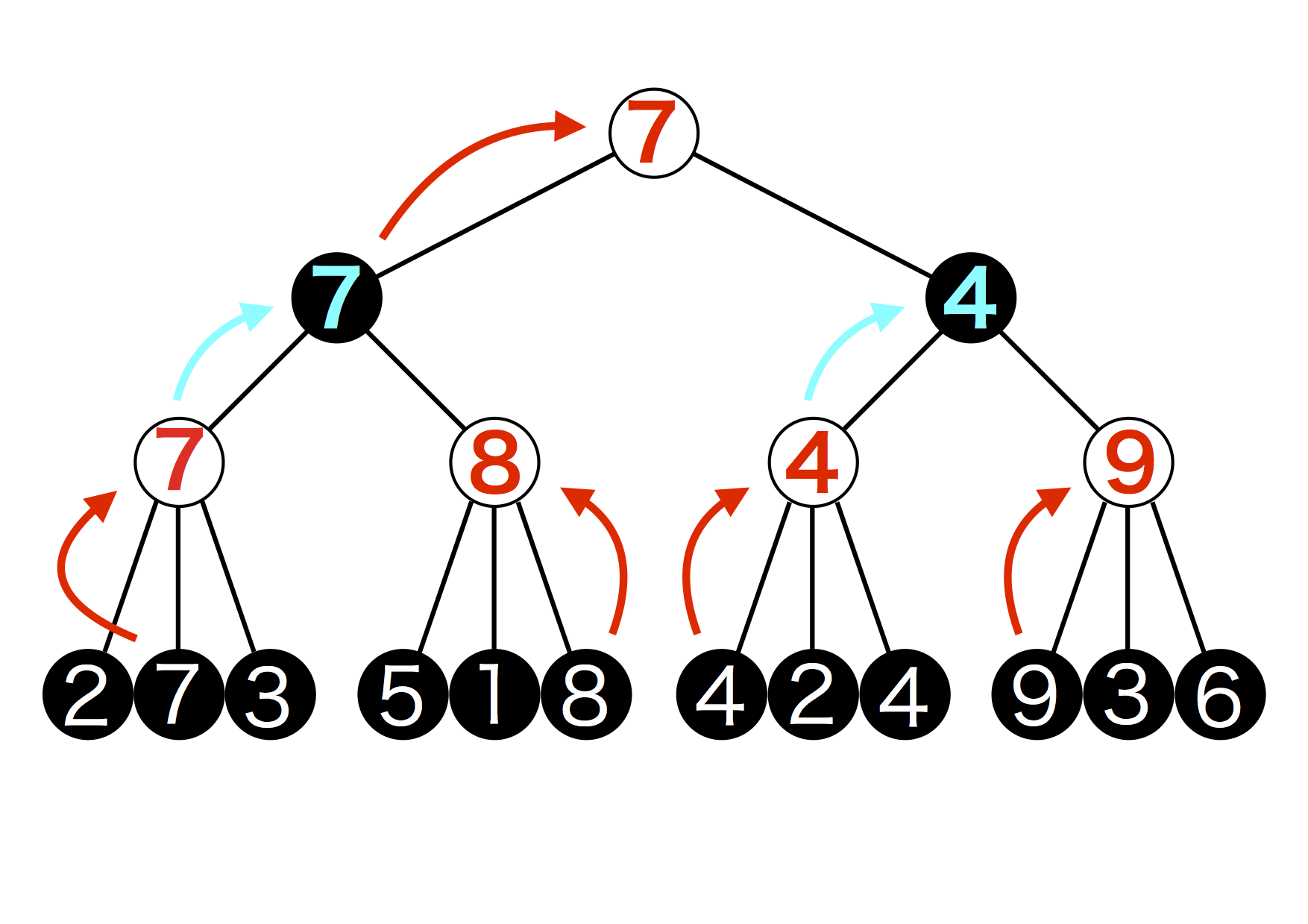
図5.6: ゲーム木6

このように、互いに最適な手を打ち続けるという仮定の元に自分にとって最も有利になる手を選ぶのがミニマックス法です。

α-β法について

ミニマックス法についてはおわかりいただけましたか？今回採用したα-β法はミニマックス法をもう少し効率化したものです。ミニマックス法そのままだと無駄な部分があるのです。それを解消したものがα-β法で、αカットとβカットと呼ばれる効率化の手段を取っています。これらは簡単に言うと「無駄な先読みをしない」ということです。

αカット

まずはαカットから。まず図を見ていただきましょう。(ゲーム木7)

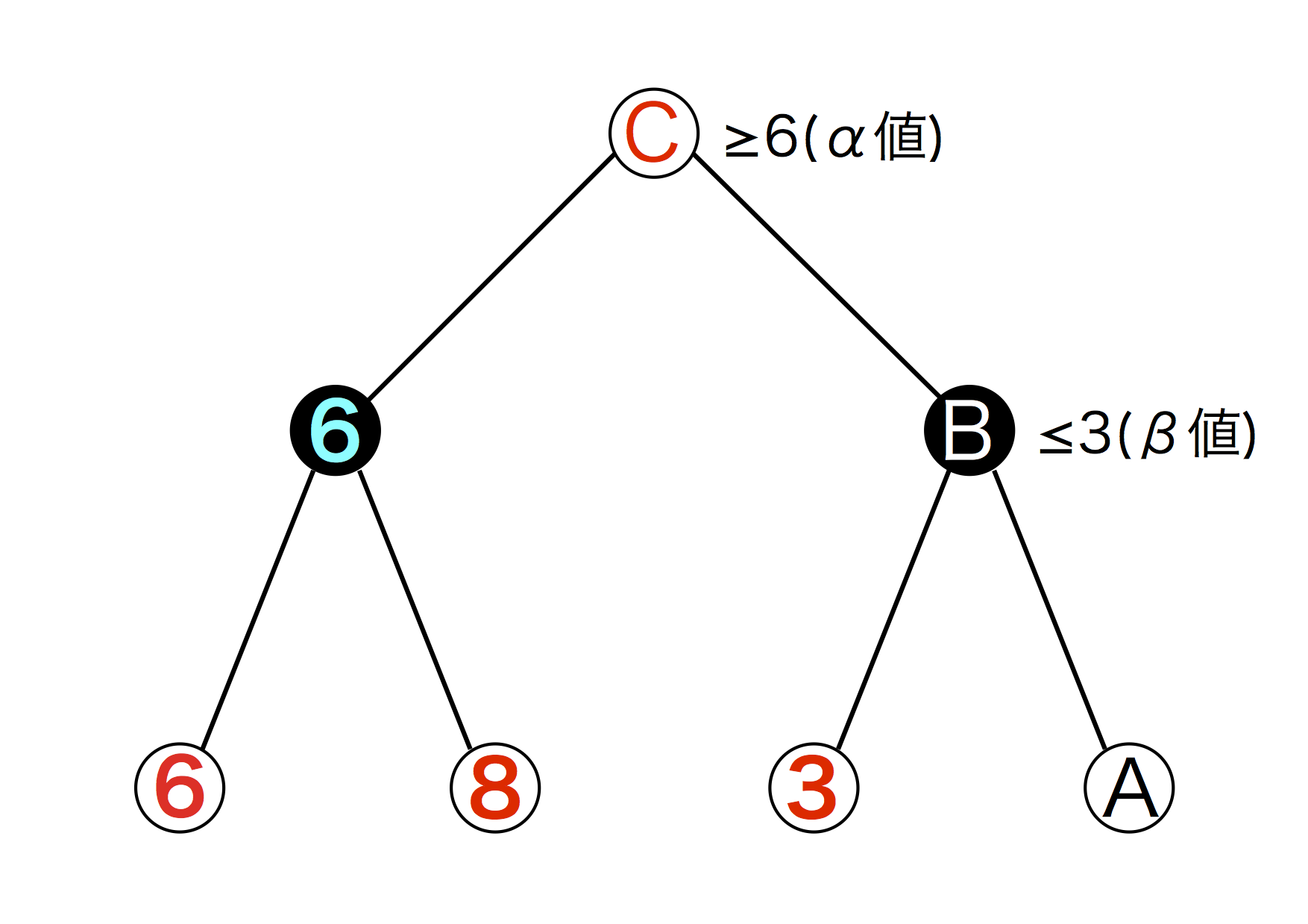
図5.7: ゲーム木7

この図におけるCを求めたいとします。そして数字が入っているところは既に数字が導かれているとします。すると、CとBにおいて C \geq 6 と b \leq 3 が成り立ちますね。この時の6をα値、3をβ値と呼びます。すると、Cは6とBのうち大きい方を選ぶので、当然6を選びます。B \leq 3 なのでBは絶対に選ばれません。するとAを調べなくともBが選ばれないことがわかります。すなわち、Bより先を読む必要性がないということです。これで無駄が削れますね。

βカット

次にβカット。これはαカットの逆ですね。図を見ればわかると思います。(ゲーム木8)

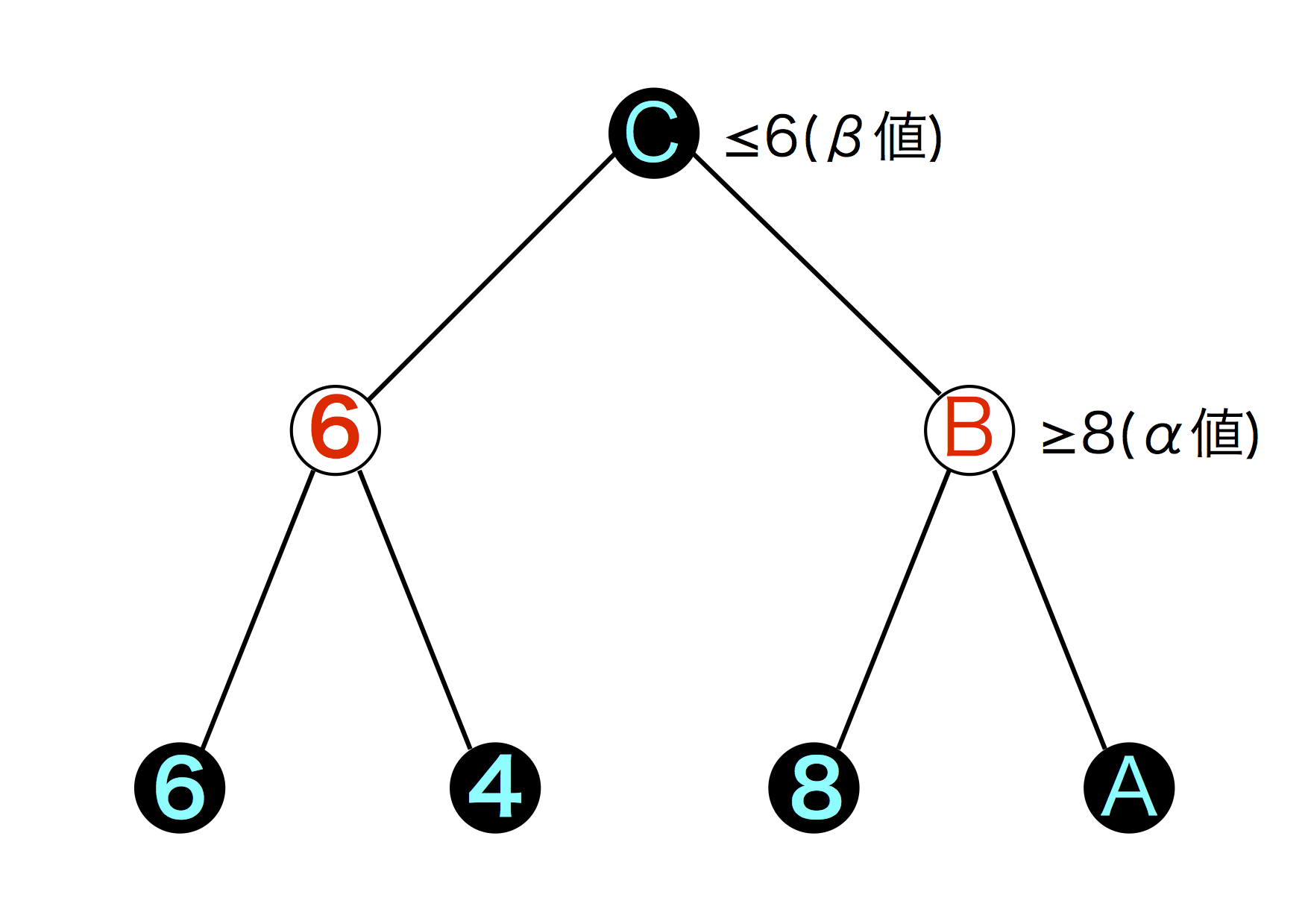
図5.8: ゲーム木8

注意して欲しいのは白と黒が逆転していることです。今回はAIではなくプレイヤーの立場に立って探索するものとします。これも同じくCを求めたいとします。数字を全て既出のものとすると C \leq 6 と B \geq 8 が成り立ちます。Cは6とBのうち最小のものを、Bは8とAのうち最大のものを選択するからですね。すると、Cは必ず6を選びます。 B \geq 8 なので常に 6 \leq B が成り立つからです。αカットと似たような感じです。するとAを調べる必要はなく、Bより先を探索する必要が無くなります。これがβカットです。

αカットとβカットは先読みする回数を減らして処理を高速にする方法です。(俗にこの操作を「枝刈り」と呼びます)ミニマックス法と比較すると高速になってることがわかります。具体的には、ミニマックス法だと3手先まで読むのが限界(これを超えると処理が重くなりすぎてPCが固まる)だったのですが、α-β法に書き換えてからは5手先まで読むことができるようになりました。処理が軽くなるとより先の手まで読むことができるようになり、結果、より強いAIが出来上がるという寸法です。ミニマックス法やα-β法など、探索のやり方はいろいろありますが、それら探索アルゴリズムの中から効率的なものを選択して使用することでAIに限らず、より早く効率的なものが出来上がります。

α-β法の実装

うだうだと書いてきましたがようやくコードです。コードを参照しながら具体的に話を進めていったほうがわかりやすいですしね。

float Search(bool isAI, int depth, float alpha, float beta){

  // ノードの評価値
  float value;

  // 子ノードの評価値
  float childValue;

  // 最終的に石を置く場所
  int bestX = 0, bestY = 0;

  if (depth == 0) {
    return Eval ();
  }

  // プレイヤーが打つときは自分にもっとも不利な手を打ってくると仮定した上で、
  // AIが打つときは自らの利益を最大にしたいので、
  // AIの手番では最小値、プレイヤーの手番では最大値をはじめに代入しておく
  value = (isAI) ? Mathf.NegativeInfinity : Mathf.Infinity;

  for (int x = 0; x < 5; x++) {
    for (int y = 0; y < 5; y++) {
      if (stoneHeight [x, y] < 5) {

        // 石を置く
        field [stoneHeight [x, y], x, y] = (isAI) ? -1 : 1;

        // 石を置ける高さを追加
        stoneheight [x, y] += 1;

        // 再帰する
        childValue = Search (false, !isAI, depth - 1, alpha, beta);

        if (isAI) {
          if (childValue > value) {
            value = childValue;
            alpha = value;
            bestX = x;
            bestY = y;
          }

          // βカット
          if (value > beta) {
            stoneHeight [x, y] -= 1;
            field [stoneHeight [x, y], x, y] = 0;
            return value;
          }
        } else {
          if (childValue < value) {
            value = childValue;
            beta = value;
            bestX = x;
            bestY = y;
          }

          // αカット
          if (value < alpha) {
            stoneHeight [x, y] -= 1;
            field [stoneHeight [x, y], x, y] = 0;
            return value;
          }
        }

        // 試しに打った石を元に戻す
        stoneHeight [x, y] -= 1;
        field [stoneHeight [x, y], x, y] = 0;
      }
    }
  }

  if (depth == searchDepth) {
    finish (-1, bestX, bestY);
    return 0;
  } else {
    // 子ノードから継承した値を返す
    return value;
  }
}

変数の説明します。

isAI

手を打つのがAIかどうか

depth

先読みする手数、深さ

alpha, beta

αカット、βカットで使用するα値とβ値

value, childValue

各ノードの評価値と、子ノード(1つ下の階層のノード)の評価値

bestX, bestY

最終的に石を置く場所のX座標とY座標

Eval()

評価関数。後述するが、盤面の点数を返す関数

stoneHeight [x, y]

任意のX,Y座標の石が置ける高さ。すでにもう置けない状態の場所は探索ができないので。

field [a, b, c]

任意の座標の状況を表す数値。1だと黒石、-1だと白石が置いてあり、0だと石が置いてないことを表す。ちなみに field [z座標, x座標, y座標] で位置を表している

AIは試しに打てる場所に手を打っていって、読む手数まで来ると盤面の評価をします。そして打った時の点数をchildValueに代入していって、その中からもっとも点数が高いものをvalueに代入します。もちろん、敵が打つ番の時はもっとも点数が低いものを返します。ここまでで理解していただけると(説明する手間が省けて)めっちゃ助かりますが、それは幻想なので(誰かこの幻想をぶち殺して)ゲーム木を使います。

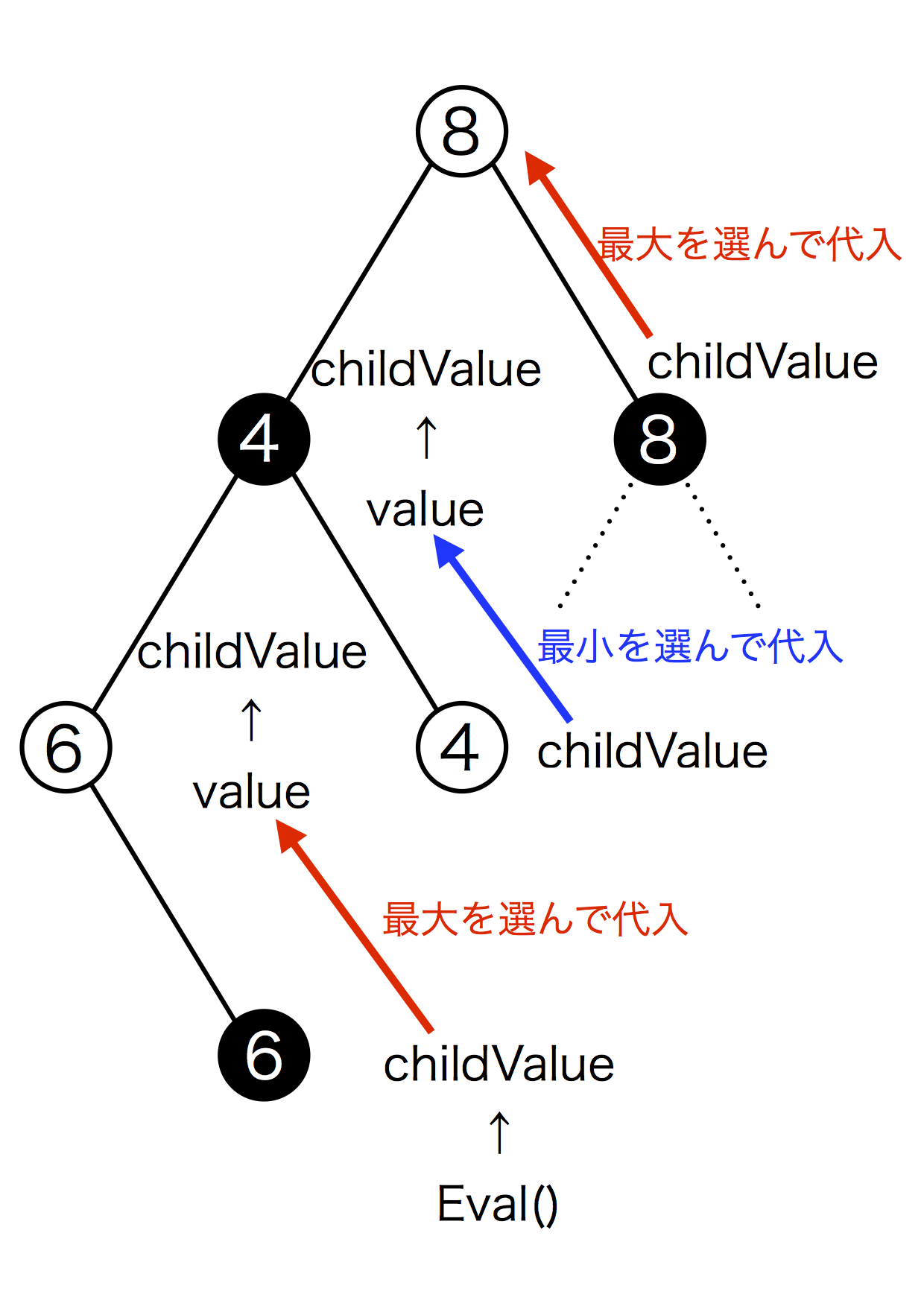
図5.9: ゲーム木9

最下層(一番下のノード)でEval関数を実行して盤面の評価をします。その値をchildValueとして受け取り、子ノードの中からもっともchildValueの値が大きい(または小さい)ものをvalueに代入します。このvalueが各ノードの数値ですね。その操作をもう1つ上の階層でも行います。この際、先ほど確定したvalue値はchildValueとして扱われます。この操作を繰り返していって一番上の階層まで到達すると探索終了です。ゲーム木9の図はこれらの操作を図式化したものです。これでα-β法の説明を終わりたいと思います。

評価関数

さて、探索のお話は終わりました。ここからは評価関数のお話です。

評価関数とは？

概要のところで、「盤面の状況を判断」と書きましたね。状況を判断というのは具体的には「自分がどれだけ有利(または不利)か判断する」ということです。どちらの石がどこにあるかを見るだけではいけません。有利さや不利さを判断しなければ戦局を把握したとは言えないでしょう。

そこで評価関数の出番です。有利さや不利さを判断するのにはやはり数字が必要ですね。自分にとって有利だと正の値で不利だと負の値。値が正、または負の方へ大きくなっていくと有利、または不利になっていくという感じです。その数字を「点数」と呼びます。盤面を見て点数をつけるのが評価関数の役目です。いくら探索アルゴリズムが優れていても、この評価関数がダメダメだと弱いAIになってしまいます。意外と大事なものなのです。なぜなら、いかに何手先を読もうとも、リーチされていることに気付かず放置するようなAIは弱いでしょう。探索アルゴリズムと並んで重要なものです。

点数をつける

評価関数の機能である点数付け。点数をつけるには規則が必要ですね。どういう状況で何点つくのか。文章書くのがめんどくさくなってきたので図で済ませます。

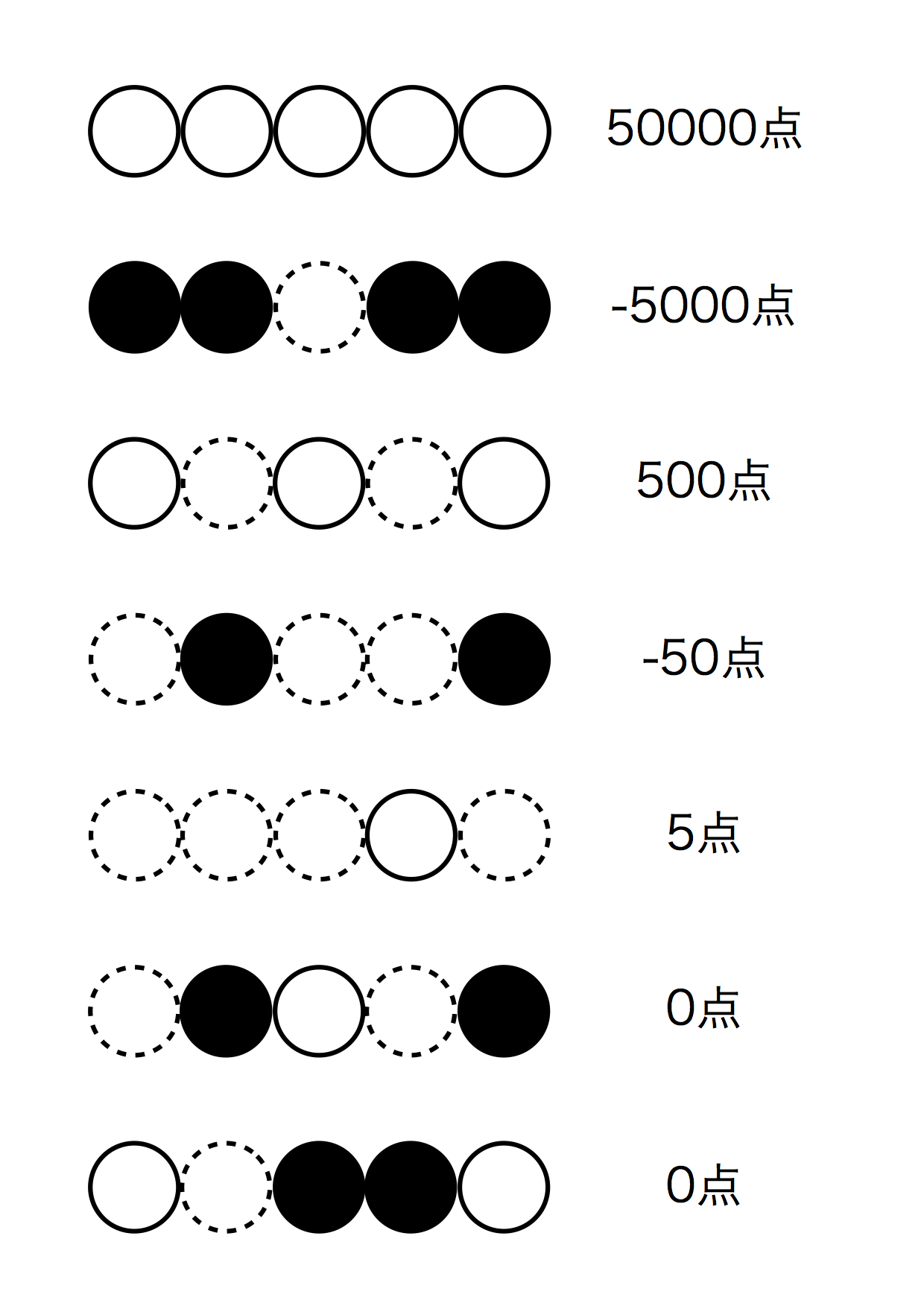
図5.10: 評価関数

このように、黒と白が同じ列にあった場合はどう頑張っても5個並べることはできないので0点で、黒は負の数、白は正の数となっています。もちろん、同じ列に同じ色の石がおいてあると点数がつき、石の数が多いほど点数は高くなっていきます。なお、この評価関数はAIが白であった場合です。AIが黒の時は点数の符号を逆転すれば良いです。点数のつけ方についてはこんなものですかね。

評価関数の実装

コード載せたいんですが、正直なところ長すぎて3ページを超えてしまうのでやめときます。とりあえず、こんな感じで実装しました。

for (int i = 0; i < 3; i++) {
  for (int x = 0; x < 5; x++) {
    for (int y = 0; y < 5; y++) {
      for (int z = 0; z < 5; z++){
        ...//石の色と数をチェック

      }
    }
  }
}

return value; //valueは盤面の点数

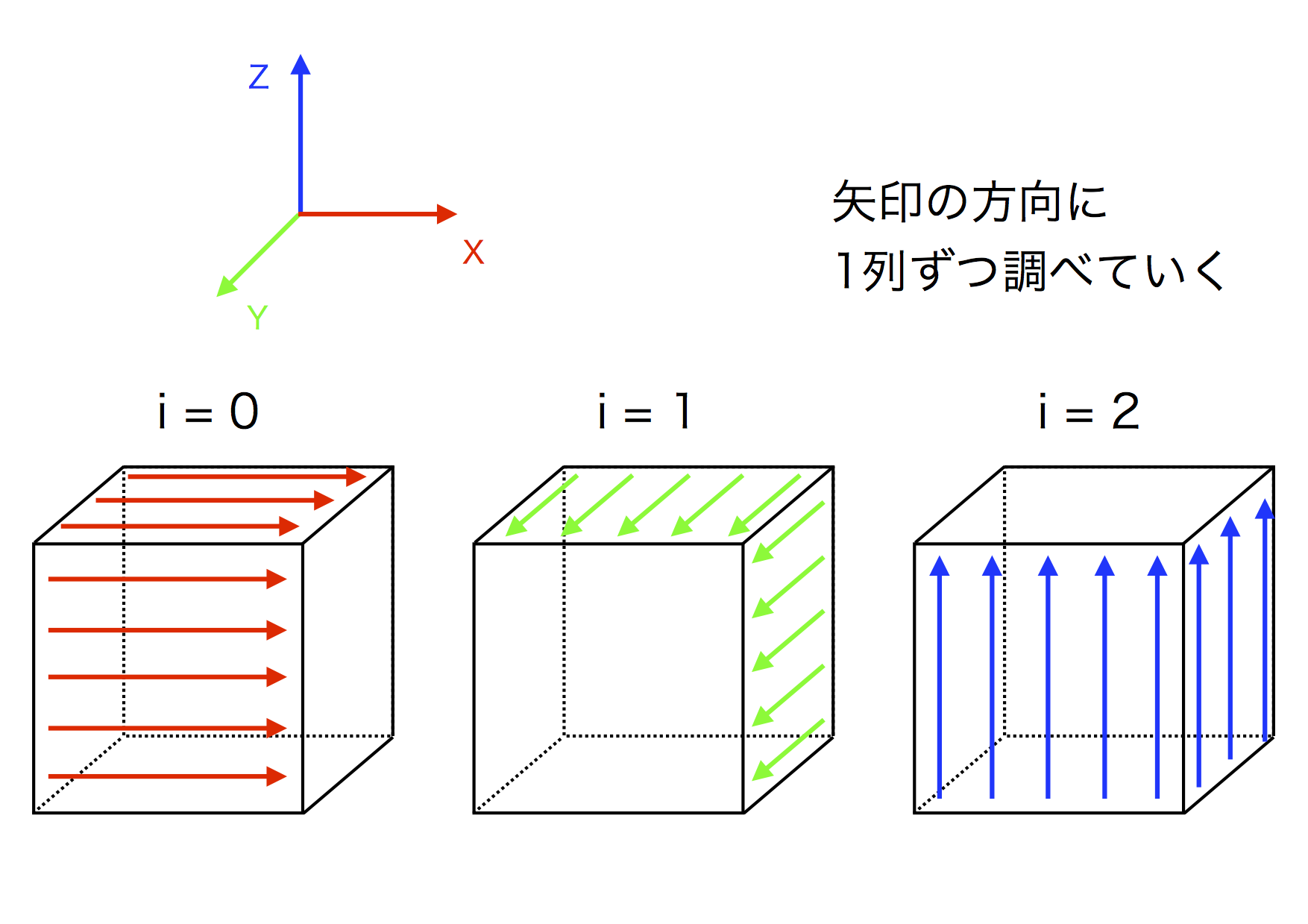
図5.11: 評価関数

この図には対角線や斜めが含まれていませんが、まぁだいたいこんな感じの実装です。1列ずつ石の色と数を調べていくだけの単純なロジックですね。あとは、 i の値によって [x, y, z] の順番を入れ替えていくと図のような感じになります。つまり、 x, y, z それぞれの方向に伸びる25列をチェックしていくということです。α-β法で使った(評価関数でも使うけど) field で表すと

i = 0

field [x, z, y] の値をチェック

i = 1

field [y, x, z] の値をチェック

i = 2

field [z, y, x] の値をチェック

ってことです。こうすることで、 x, y, z 方向の列が順にチェックできます。あとはチョチョイっと対角線を調べてしまえば点数が出ますね。これぐらいで評価関数のお話は終わりにしたいと思います。

5.4　思考力のネクローシス

さて、これまでα-β法と評価関数のお話をしてきました。α-β法はともかく、僕自身、評価関数のコードを気に入っていません。for 文を何重にも重ねたなんとまぁ愚直なコード。なんとなくですが、効率が悪そうな気がします。これでも改良を重ねたのですが、なかなかすっきりとしたコードが書けませんでした。精進が足りないということでしょうか。

ではここで評価関数について言い訳を始めます。まず、立体5目並べということで、勝ち方つまり勝つための石の置き方が通常の5目並べより相当多いです。具体的には109通りです(多分)。しかも、一直線のものもあれば、立方体の対角線上に並べるものもあります。正直なところ綺麗なロジックが組めません。僕の頭が硬い(諸説あるが脳筋ゴリラ。数学などでもゴリ押しで解く)せいもあるかもしれませんが。

言い訳終わり。とにかく、完璧なコードではありません。これから精進して、美しいコードをかけるようになりたいと思います。

5.5　能力値のメルト

さて、ここからは余談です。もちろん今回のお話とは全く関係はございませぬ。余談といっても単なる身の上話なので興味のない人は読み飛ばしていって構いませんよ。

僕は中2の6月頃にこの部活に入部しました。それまでの1年半ほどは学校に行き、家に帰ってゲームをして、また学校に行くという生活を送っていました。その時の僕は大した目標もなく、さしてやりたいこともありませんでした。そんな時期に入部した動機は「当時同クラだった部長に誘われたから」と「気まぐれ」です。初めの頃は何をやったらいいかわからなかったのでC言語の勉強をしていました。でも割とすぐに飽きてしまってそこからしばらくは何もしていませんでした。そこから夏休みに入り、ただただ時間を浪費していたのですが、夏休みの終わり頃に Unity と出会いました。最初はボールが動くだけでなんだか楽しくなってどんどん進んで行きました。夏休みが明けると文化祭の準備が少しずつ始まって行きます。初めは何もしていませんでしたが、これでは何だかこの部にいる意味を感じないなぁと思い、思い切って仕事を受けることにしました。 Unity と Kinect を使ったゲームの案があったのでそれを受けましたね。そこからはもう必死で Unity の勉強をして文化祭に間に合わせようとしまして、まぁ準備期間注も Red Bull と魔剤に頼って頑張りました。めっちゃ疲れたんですが、とってもやりがいがあって楽しかったです。この時僕は中学3年。遅すぎる文化祭初参加でしたw

中3の夏、合宿を通して色々な分野に興味が出ました。そう、この時は中3の間、高校生になるまでにどんなことを勉強しようとか身につけようとしか考えていませんでした。

夏休みが明け、2学期がスタートしました。ある日、学校の後、塾に行き、休み時間でスマホをいじっていた時です。

びっくりです。いきなり部長とか言われて困っちゃいました。どういう経緯でそうなったかも分かりませんし。結局その後の授業は全く頭に入ってきませんでした。

とりあえず経緯を聞くと部長が生前退位の意向を示されたため、後任を探していたところ、僕になったみたいです。僕には荷が重いと思いました。何せ僕は部に入って1年ちょっとしか経っていなかったのですから。でも、他に次期部長候補がいないなら、ということで部長を受けました。そこからが大変でした。部に在籍している期間が短い分、わからないことが多すぎたのです。特に各種イベントや文化祭関連が意味不明でしたね。文化祭を1度経験しているといっても、その時はひたすら自分の展示の調整をしていたのでその時の部長が何をしていたかなんて知らないわけですから。さらに、引き継ぎがとても雑。いや、雑というよりは雑にならざるを得なかったんですよね。昔の部員たちは文化祭や部運営に間することを一切文書化せず、引き継ぎもせず卒業していったので、そういったノウハウが受け継がれていませんでした。そういうわけでまずはマニュアル作りから始まりました。他の部員たちの力を借りてなんとかある程度マニュアルが完成したと思ったら、もう予算折衝の時期です。来年度の部の予算を決めるのが予算折衝ですが、もちろん僕はそのようなことは全く知りませんでした。とりあえず、予算をぶんどるために必死で物品の必要性を主張すると意外となんとかなっちゃいましたw

さて、ここから文化祭準備、つまりこの記事を執筆している期間ですね。部長の仕事のメインです。正直なところ、マニュアルとか僕の代だけの特例だし、予算折衝はまぁ1日限りだしで、部長の仕事は文化祭期間中だけといってもいいぐらいですね。書類を書いて提出したり、集会に出席したり……

で、現在に至るわけです。ここまで、部長職をこなす上で多くのことを経験してきました。顧問と物品購入について相談したり、生徒会役員と色々なやり取りをしたり。大変でしたが得るものはあったと思います。視野が広がったというかなんというか。とりあえず現状の目標も決まりました。

しかし、目標が定まってしまうとこれまた厄介なことに、部長職というのが煩わしくなってくるんです。やりたいことがあるのに部長職で時間が削られる。部長職は自分にとって様々なものをもたらしてくれたけれど、部長職そのものがやりたいわけではない。困りものですね。ようやく前部長が部を去った理由が理解できました。彼は既に、自分の興味の向く先を把握して、行動していたのです。僕がそれを得るまでに相当時間がかかってしまいました。だってもう高校生ですよ？残された時間がもう少ない年頃に、今更気づいたことを今では後悔しています。なんで中1から中2まで何もして来なかったんだろう、とか。なんでもっと早く気づけなかったんだろう、とか。僕にはもう残された時間は少ないです。あ、別に死にませんよ。高3になれば否応無く受験勉強がやってきます。高校生なので少しずつでも受験の準備を進めていくために、勉強時間も増やさなければいけません。やりたいことをできる時間はもう少ないのです。だから、中学に入ってからの生き方を、今は後悔しています。

さてさて、身の上話はこれでおしまい。タイトルをつけるなら、そうだな、「今更遅い、年寄りの後悔」って感じですね。なんでこんな長ったらしい話を書いたかというと、まぁ自分の中に溜め込んでた感情を吐き出したかったんですよね。だってこんな話、誰もまともに聞いてくれないじゃないですかwだからこの場を借りて、自分の気持ちを吐露して、これから進んでいきたいと思ったわけです。ここまで読んでいただいたら僕も嬉しいです。これからも精進していきたいと思います。

5.6　終わりと始まりのプロローグ

ここまで読んでいただき本当にありがとうございます。ついでに僕の将来の夢的な何かをここで言っときます。

僕はこれが1番だと思っています。なんの変哲のない人生でも、人並みに幸せに過ごせたら僕はそれで満足です。

どうでもいい話でしたねw では、これからもNPCAをよろしくお願いします〜