第3章　「計算量」 by taizo0122 (72)

3.1　はじめに

自己紹介と説明

あの小冊子からわざわざ本編にお越しいただいてありがとうございます。72回生のtaizo0122です。なぜか高校生になりました。最近時間の流れの速さに恐ろしさを感じています。中学時代はなかなか実のない生活を送っていたので、高校生のうちに世界に羽ばたく素晴らしい人間になりたいと思っております。

この記事では、競技プログラミングにおける基本的で有名で便利な考え方を説明していきます。（といっても、NPCAに好き好んでくるような方々にとっては知っていて当たり前の内容かもしれません。）文中のソースコードは100パーセントC++で書かれています。多少雑多なソースコードになっているかもしれませんがご了承ください。もしC++がわからなくても、考え方ぐらいは見てもらえると嬉しいです。

競技プログラミングとは

みなさん、競技プログラミングというものをご存知でしょうか。普通だと、何かのサービスやソフトを作ることを目的にプログラムを組むんですが、競技プログラミングは、

競技プログラミングでは、参加者全員に同一の課題が出題され、より早く、与えられた要求を満足するプログラムを正確に記述することを競う。コンピュータサイエンスや数学の知識を必要とする問題が多い。新卒学生の採用活動などに使われることもある。多くのコンテストでオンラインジャッジが採用されている。(Wikipediaより)

らしいです。競技プログラミングには、プログラム自体の正誤以外にも、時間制限、メモリ制限があります。そのため、正しいプログラムを書くこと以外にも、速くて軽いプログラムを書くことも求められているわけです。

図3.1: 時間制限

図3.1のように、問題ごとに時間、メモリ容量が制限されています。

今回の部誌では競技プログラミングと計算量について説明しようと思います。計算量というのは、

アルゴリズムの計算量(けいさんりょう)とは、計算機がそのアルゴリズムの実行に要する計算資源の量をいい、アルゴリズムのスケーラビリティを示す。(Wikipediaより)

らしいです。Wikipedia先生ありがとうございます。要するに、プログラムを実行するときにかかる時間を表す指標です。同じ問題を解くに当たっても、プログラムが違えば実行にかかる時間も変わります。

計算量には、実行にかかる時間を表す時間計算量と、実行に使うメモリの量を表す空間計算量の２種類があるのですが、今回は時間計算量を取り扱うので、「計算量」と書いているところは「時間計算量」とみなしてください。

ちなみに、計算複雑性理論については、P=NP問題とかなんか色々有るんですが、そんな難しいことは書かないです(というか書けません)。

3.2　計算量のいろは

計算量が違うパターン

計算量は、先程も言ったとおり、プログラムを実行するのにかかる時間を表す指標のことです。「プログラムが違うと実行にかかる時間も変わるってどういうこと?」という話ですが、例えば、1からNの総和を求めるとします。

素直に計算する
公式を使う

素直に計算すると(N-1)回の足し算が必要ですが、(1+N)*N/2の公式を使えば、足し算掛け算割り算の計3回で済みます。こんな感じで、計算方法によってかかる時間は変わります。ちなみに、ガウスは2つめの計算方法を小学生の時に思いついたそうです。ちょっと意味がわからないですね。

O記法

計算量はOという記号を用いて表します。幾つかのルールが有るので、説明しておきます。

最大次数の項のみを残す
係数は1にする

例:

O(N-1) → O(N)
O(2N^2+4N) → O(N^2)
O(2^N+N^2) → O(2^N)
O(N+M) → 違う変数はまとめられない

(理由)計算量は、入力サイズが大きい場合を想定しているので、最大次数以外の項は計算量にあまり影響を及ぼさないからです。

(例) O(N^2+N)の場合

N=1 → 2
N=1000 → 1001000
N=1000000 → 1000000001000

このように、Nが大きくなるにつれてO(N^2)とほとんど等しくなります。また、定数倍程度の違いは無視できます。

ここまでの説明で、競技プログラミングや計算量についてある程度のことはわかったと思います。次の章からは、冒険者キョウ=ギ君といっしょに具体例を交えて学んでいきましょう。

3.3　あらすじ

この世に、自分が異世界を冒険する妄想を一度もしたことがない人間はいないでしょう（たぶん）。人類はみな冒険が好きなのです。昔々、ある世界に、物事を全てアルゴリズムで考えてしまう天才頭脳の冒険者キョウ=ギ君がいました。彼は、どんな事件も持ち前の頭脳と戦闘スキルで解決してしまう、文武両道のすご腕冒険者です。この記事は、そんなキョウ=ギ君の伝説を記す英雄譚である---

3.4　冒険者の生活

おなかがすいた

伝説の冒険者といえども、おなかは減ります。にんげんだもの。キョウ=ギ君は今町で一番人気の食堂にいます。この食堂は、メニューの豊富さで有名です。食事のメニューごとに満腹度と満足度が与えられるので、満腹度がキョウ=ギ君の限界を超えないように選んだときの、満足度の合計の最大値を求めます。

まずは、各メニューに対し食べるか食べないかで分岐しながら探索をしてみます。

#include <cstdio>
#include <algorithm>

using namespace std;

const int MAX_N=100;

int n,W;//n:メニューの個数　W:キョウ=ギ君のお腹の容量
int w[MAX_N],v[MAX_N];//w:満腹度　v:満足度

 //i番目以降のメニューから満腹度の合計がj以下になるように選ぶ
int solve(int i, int j) {
  int res;//res:満足度の合計
  if (i == n) {
    // 全てのメニューをチェックし終えたときは、満足度の合計の最大値は0で確定
    res = 0;
  } else if (j < w[i]) {
    // お腹の容量が足りないので食べない
    res = solve(i + 1, j);
  } else {
    // メニューiを食べるか食べないかを選び、満足度の高い方を選択する
    res = max(solve(i + 1, j), solve(i + 1, j - w[i]) + v[i]);
  }
  return res;
}

int main(){
  scanf("%d%d",&n,&W);
  for(int i=0; i<n; i++){
                scanf("%d%d",&w[i],&v[i]);
        }
  printf("%d\n",solve(0,W));
  return 0;
}

この方法だと、探索の深さはメニューの個数であるn、各深さにおいて食べるか食べないかの2通りの分岐が発生しており、O(2^n)となってしまいます。実は、このアルゴリズムだと、同じsolve(i,j)が何度も呼び出される可能性があります。同じsolve(i,j)に対して何度も計算をする必要は無いので、最初の計算結果を記憶するようにしてみます。

#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

const int MAX_N=100;
const int MAX_W=1000;

int n,W;
int w[MAX_N],v[MAX_W];
int dp[MAX_N + 1][MAX_W + 1];

int solve(int i, int j){
  if(dp[i][j]>=0){
    // すでに調べていた場合その結果を利用
    return dp[i][j];
  }
  int res;
   if (i == n) {
      res = 0;
    } else if (j < w[i]) {
     res = solve(i + 1, j);
    } else {
     res = max(solve(i + 1, j), solve(i + 1, j - w[i]) + v[i]);
    }
  return dp[i][j]= res;
}

int main(){
  scanf("%d%d",&n,&W);
  for(int i=0; i<n; i++){
    scanf("%d%d",&w[i],&v[i]);
  }
  memset(dp, -1, sizeof(dp));//-1はまだ調べていないことを示す
  printf("%d\n",solve(0,W));
  return 0;
}

この改良によって、同じ引数では最初の１回しか再帰呼び出しが行われず、引数の組み合わせはnW通りしかないため、O(nW)となりました。このように、テーブルを作り、そこで値を保持しておく手法はメモ化と呼ばれます。このメモ化テーブルについて、

dp[i][j]:i番目以降のメニューから満腹度の合計がj以下となるように選んだときの満足度の合計の最大値

とすると、

dp[n][j]=0;

dp[i][j]=\begin{cases}dp[i+1][j] & (j<w[i]) \\ max(dp[i+1][j],dp[i+1][j-w[i]]+v[i]) & (j \geq w[i]) \end{cases}

という漸化式が成り立ちます。再帰関数の代わりに、直接この漸化式を適用して計算していくことで、単純な2重ループで問題が解けます。このように、漸化式を適用するなどして順に解を求めていく手法を動的計画法(Dynamic Programming)、つまりDPといいます。

#include <cstdio>
#include <algorithm>

using namespace std;

const int MAX_N=100;
const int MAX_W=1000;

int n,W;
int w[MAX_N],v[MAX_N];
int dp[MAX_N + 1][MAX_W + 1];

void solve() {
  for (int i = n - 1; i >= 0; i--) {
    for (int j = 0; j <= W; j++) {
      if (j < w[i]){
        dp[i][j] = dp[i + 1][j];
      }
      else{
        dp[i][j] = max(dp[i + 1][j], dp[i + 1][j - w[i]] + v[i]);
      }
    }
  }
  printf("%d\n",dp[0][W]);
}

int main(){
  scanf("%d%d",&n,&W);
  for(int i=0; i<n; i++){
    scanf("%d%d",&w[i],&v[i]);
  }
  solve();
  return 0;
}

この方法でも、先ほどと同じくO(nW)になりますが、見た目はこちらのほうがきれいですね。しかし、キョウ=ギ君がとんでもない大食漢だった場合、このアルゴリズムだと時間がかかってしまいます。そこで、逆に満足度に対する最小の満腹度を求めてみましょう。

dp[i+1][j]:i番目までのメニューから満足度の合計がjとなるように選んだときの満腹度の合計の最小値(そのような解が存在しない場合は十分大きな数INF)

とすると、i番目までのメニューから満足度の合計がjになるような選び方は、

i-1番目までのメニューから満足度の合計がjとなるように選ぶ

i-1番目までのメニューから満足度の合計がj-v[i]となるように選び、i番目のメニューを追加する

の２通りがあるので、

dp[0][j]=INF

dp[0][0]=0

dp[i+1][j]=min(dp[i][j],dp[i][j-v[i]]+w[i])

という漸化式が成り立ちます。最終的な答えは、dp[n][i] \leq Wとなる最大のjになります。

#include <cstdio>
#include <algorithm>

using namespace std;

#define INF 12345678910
const int MAX_N=100;
const int MAX_V=100;

int n,W;
int w[MAX_N],v[MAX_N];
int dp[MAX_N + 1][MAX_N*MAX_V + 1];

void solve() {
  fill(dp[0], dp[0]+MAX_N*MAX_V + 1, INF);
  dp[0][0]=0;
  for(int i=0; i<n; i++){
    for(int j=0; j<=MAX_N*MAX_V; j++){
      if(j < v[i]){
        dp[i+1][j]=dp[i][j];
      }else{
        dp[i+1][j]=min(dp[i][j], dp[i][j-v[i]]+w[i]);
      }
    }
  }
  int res = 0;
  for(int i=0; i<=MAX_N*MAX_V; i++) if(dp[n][i]<=W) res = i;
  printf("%d\n",res);
}

int main(){
  scanf("%d%d",&n,&W);
  for(int i=0; i<n; i++){
    scanf("%d%d",&w[i],&v[i]);
  }
  solve();
  return 0;
}

この場合の計算量はO(n Σi v[i])となります。このように、問題の条件によって多少の変更を加えることも必要です。

世界を救え！

グラフについて

この章ではグラフの概念を使うので、基本的な用語などを説明しておきたいと思います。

グラフって何？

アルゴリズムを考える際には、グラフという考え方が非常に便利です。ここで言うグラフは、頂点(node)と辺(edge)からなるもののことです。頂点は対象を、辺は頂点同士の関係を表します。頂点の集合がV、辺の集合がEであるグラフをG=(V,E）と表し、2点u,vを結ぶ辺をe=(u,v)と表します。また、わかりやすくするために頂点の個数を|V|、辺の個数を|E|と表現します。

有向グラフと無向グラフ

グラフには有向グラフと無向グラフの２種類があります。e=(u,v)が存在する時、u→vとv→uどちらの方向にも移動できるものを無向グラフ、u→vの方向のみにしか移動できないものを有向グラフといいます。簡単にいえば、有向グラフは一方通行で、両方の向きに進めるのが無向グラフです。

歩道、路、閉路

隣接している頂点同士を辿った道筋を歩道(walk)といいます。そのうち、始点と終点が異なり、通る辺が重複しないものを路(path)といい、始点と終点が同じで、通る辺が重複しないものを閉路(cycle)といいます。

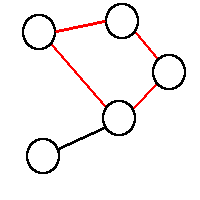
図3.2: 閉路のグラフ

グラフの表現

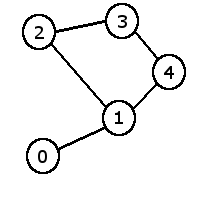
図3.3: 行列、リスト

図3.4: 行列

図3.5: リスト

隣接行列

|V|*|V|の二次元配列でグラフを表したものを隣接行列といいます。graph[i][j]には、e=(i,j)の有無、e=(i,j)のコストなどを入れておきます。O(1)で辺の有無を判定できるなどの利点はありますが、常にO(|V|^2)のメモリを消費し、無駄な部分も多くなってしまいます。

隣接リスト

頂点ごとに、隣接する頂点を(C++の場合は)vectorなどで管理したものを隣接リストといいます。こちらの場合なら、メモリはO(|V|+|E|)しか消費されません。

決戦

どうやら、遠くの町に大魔王が現れたようです。名高い冒険者であるキョウ=ギ君は召集を受けました。急ぐキョウ=ギ君は、遠くの町までの最短距離を求めます。

まず、町同士の関係を先ほど説明したグラフに置き換えてみると、頂点が町、辺が町同士をつなぐ道を表すことになります。問題の都合上、道が通っていない町同士を移動することはできないとします。（伝説の冒険者なら空くらい飛べるだろという突っ込みはご法度）始点であるキョウ=ギくんの住む町はs番とします。キョウ=ギくんの住む町sから他の町iへの最短距離をd[i]とすると、

d[i]=min{d[j]+(jからiへの道の長さ)}(jはiと道でつながれている任意の町)

が成り立ちます。なので、

初期値　d[s]=0

d[i]=INF(十分大きな数)

として、上の式を適用してdを更新していきます。このアルゴリズムをベルマンフォード(Bellman-Ford)法といいます。

#define INF 12345678910
const int MAX_V = 100;
const int MAX_E = 100;

struct road{int from, to, cost;};//from:出発する町　to:到着する町　cost:道の長さ
road es[MAX_E];// 道
int d[MAX_V];//i町への最短距離
int V,E,s;//V:頂点の数　E:道の数　s:最初の町

void BellmanFord(int s){
  fill(d,d+V,INF);
  d[s]=0;
  while(true){
    bool update = false;// 最短距離の変更があったか
    for(int i=0; i<E; i++){
      road e = es[i];
      if(d[e.from]!=INF && d[e.to]>d[e.from]+e.cost){
        // これまでに判明しているよりもさらに短いものがある場合更新
        d[e.to]=d[e.from]+e.cost;
        update = true;
      }else if(d[e.to]!=INF && d[e.from]>d[e.to]+e.cost){
        // 反対方向をチェックする部分なので、有向グラフならこのelse if部分は必要ない
        d[e.from]=d[e.to]+e.cost;
        update = true;
      }
    }
    if(!update) break;
  }
}

int main(){
  scanf("%d%d%d",&V,&E,&s);
  for(int i=0; i<E; i++){
    scanf("%d%d%d",&es[i].from,&es[i].to,&es[i].cost);
  }

  BellmanFord(s);

  for(int i=0; i<V; i++){
    if(d[i]==INF) printf("INF\n");
    else printf("%d\n",d[i]);
  }

  return 0;
}

このアルゴリズムでは、たかだか(V-1)個の辺しか通らず、while(true)のループは(|V|-1)回しか実行されません。while(true)ループの中でE回の繰り返しを行うfor文が実行されるため、計算量はO(|V||E|)となります。ただし、負の閉路が存在する場合は、このアルゴリズムは成り立ちません（|V|回目のループが起こったかを確認することで負の閉路の検出を行うことができます）。

天才頭脳のキョウ=ギ君は他の求め方も思いついてしまいました。上と同様にd[s]=0,d[i]=INFとします。そして、

1.まだ使われていない頂点の中でd[i]が最小の頂点を探す2.その頂点に隣接する頂点をd[i]=min{d[j]+(jからiへの道の長さ)}で更新し、ここで使った頂点を以後使わないようにする

を繰り返します。このアルゴリズムをダイクストラ(Dijkstra)法といいます。ただし、このアルゴリズムは負の辺がない場合のみ使えます。初期状態では、始点のみ最短距離が確定しています。まだ使われていない頂点のうちd[i]が最小の頂点は、負の辺がないという条件からd[i]がより小さくなることがないので、最短距離が確定しています。

#include <cstdio>
#include <algorithm>

using namespace std;

#define INF 12345678910
const int MAX_V=100;

int cost[MAX_V][MAX_V];//cost[u][v]はu-v間の距離
int d[MAX_V];
bool used[MAX_V];//使われたかどうか
int V,E,s;

void dijkstra(int s){
  fill(d,d+V,INF);
  fill(used,used+V,false);
  d[s]=0;

  while(true){
    int shortest=-1; //shortestは次に使う頂点の番号
    for(int u=0; u<V; u++){ // 次に使う頂点を探す
      if(!used[u] && (shortest==-1 || d[u]<d[shortest])) shortest=u;
    }
    if(shortest==-1) break;
    used[shortest]=true;

    for(int u=0; u<V; u++){ // 最短経路の更新
      d[u]=min(d[u],d[shortest]+cost[shortest][u]);
    }
  }
}

int main(){
  for(int i=0; i<MAX_V; i++){
    for(int j=0; j<MAX_V; j++){
      cost[i][j]=INF;
    }
  }
  scanf("%d%d%d",&V,&E,&s);
  for(int i=0; i<E; i++){
    int u,v;
    scanf("%d%d",&u,&v);
    scanf("%d",&cost[u][v]);
    cost[v][u]=cost[u][v]; // 反対方向をチェックする部分なので、有向グラフならこの部分は必要ない
  }

  dijkstra(s);

  for(int i=0; i<V;i++){
    if(d[i]==INF)printf("INF\n");
    else printf("%d\n",d[i]);
  }
  return 0;
}

隣接行列を用いたこのダイクストラ法の計算量は、最短経路の更新に(|V|)回、次に使う頂点を探すのに(|V|)回、合わせてO(|V|^2)となります。ここで、優先度付きキューを使って次に使う頂点を(log|V|)回で探せば、全体の計算量はO(|E|log|V|)となります。

#include <cstdio>
#include <vector>
#include <algorithm>
#include <queue>

using namespace std;

#define INF 12345678910
const int MAX_V=100;

struct edge{int to, cost;};
typedef pair<int,int> P;//first:最短距離　second:頂点の番号
vector<edge> G[MAX_V];
long long int d[MAX_V];
int V,E,s;

void dijkstra(int s){
  priority_queue<P,vector<P>,greater<P> > que;
  fill(d,d+V,INF);
  d[s]=0;
  que.push(P(0,s));

  while(!que.empty()){
    P p = que.top();
    que.pop();
    int v = p.second;
    if(d[v]< p.first) continue;
    for(int i=0; i<G[v].size(); i++){
      edge e = G[v][i];
      if(d[e.to]>d[v]+e.cost){
        d[e.to]=d[v]+e.cost;
        que.push(P(d[e.to],e.to));
      }
    }
  }
}

int main(){
  scanf("%d%d%d",&V,&E,&s);
  for (int i=0; i<E; i++) {
    int from, to, cost;
    scanf("%d", &from);
    scanf("%d", &to);
    scanf("%d", &cost);
    edge e;
    e.to = to;
    e.cost = cost;
    G[from].push_back(e);
  }

  dijkstra(s);

  for(int i=0; i<V;i++){
    if(d[i]==INF)printf("INF\n");
    else printf("%lld\n",d[i]);
  }
  return 0;
}

この方法なら、ベルマンフォード法のO(|V||E|)よりも高速に計算することが出来ます。ただし、負の辺が含まれる場合は使えないことには注意が必要です。また、この問題も1章と同じように、問題の条件や入力によってプログラムの速さは異なってきます。

そして伝説へ・・・

かくして、大魔王の討伐に成功したキョウ=ギ君はその功績を讃えられ、世界を救った英雄として永遠に語り継がれることとなりました。めでたしめでたし。

3.5　あとがき

最後までこの記事を読んでいただきありがとうございました。そしてお疲れ様でした。がんばってオリジナリティを出そうとしたら、文才がなくて余計にわかりにくくなった気がします。悲しい。厨二病感もプンプンしますね。競技プログラミングには、ここで紹介した以外にも様々なアルゴリズムや考え方がありますので、興味を持った方はぜひ調べてみてください。それでは、またお会いしましょう～

3.6　参考文献

秋葉拓哉、岩田陽一、北川宜稔(2010)プログラミングコンテストチャレンジブック [第2版]　マイナビ

第3章 「計算量」 by taizo0122 (72)

3.1 はじめに