第3章　CTF超入門

75回生 sashiming

3.1　はじめに

sashimingです。気づけば高2で、老いを感じている次第です。

普段は競技プログラミング(略称:競プロ)をたしなんでいるのですが、最近はモチベが上がらなくなってきたので、「CTF」という競技を始めてみました。CTFは競プロよりも敷居が高いので、はじめに何をするべきか分からない人が多いと思います。そこで、この記事ではCTFを最低限楽しむための基礎知識を書いていこうと思います。

3.2　注意

この部誌では、OSにWindows10を用いています。他のOSを使用しているかたは、適宜読み替えるなどしてください。

3.3　What's CTF

CTFは``Capture the Flag''の略で、サイバーセキュリティなどに関する技術や知識を活用して情報を抜き取る競技です。ハッカーのようなことをすると言っても差し支えはないでしょう。

CTFには主に2つの形式があります。

クイズ形式(Jeopardy style)*1：独立した問題がたくさん与えられるので、与えられたプログラム・Webサイト・暗号・画像などから``flag''と呼ばれる文字列を探す
攻防戦形式(Attack/Defense style)：各チームにサーバが与えられ、他のチームのサーバを攻撃してflagを奪取しながら自分のチームのサーバを防衛する

基本的に、オンラインで開かれるCTFコンテストはクイズ形式です。この記事では、クイズ形式のコンテストで出される問題について書きます。

[*1] 「Jeopardy!」というアメリカのテレビ番組が由来です

クイズ形式で出される問題にはいくつかジャンルがあります。

Reversing：与えられたバイナリを解析してflagを探す
Pwn：与えられたプログラムの脆弱性を突いてflagを奪う
Web：webサイトの脆弱性を突いてflagを奪う
Crypto：暗号を解いてflagを見つける
Forensics/Steganography：ディスクイメージや画像・音声などを解析してflagを探す
Misc：その他・雑学

3.4　例題

ここで、簡単な問題を紹介します。ジャンルはCryptoです。

わけがわからない文字列ですが、勘の良いかたは何となく見当がつくかもしれません。

答えを言ってしまうと、これはシーザー暗号と呼ばれる、最も有名かつ古典的な暗号です。仕組みはごく単純で、それぞれのアルファベットを3文字ぶん後にずらしているだけです。例えば、aはdに、eはhに、yはbに変換されます。

平文(もとの文)を3文字ぶん後にずらして暗号化しているので、復号するには逆に暗号文を3文字ぶん前にずらすだけで良いです。先ほどの暗号文を復号すると、次のようになります。

ちゃんと意味のわかる文字列になりましたね！

3.5　CTFの学習方法

CTFのコンテストが開かれるWebサイトは、コンテスト終了後閉鎖されてしまうものが多いですが、中には常に問題が公開されている「常設CTF」があります。

以下に入門レベルのかたでも取り組みやすい常設CTFを紹介しておきます。

CpawCTF (https://ctf.cpaw.site/)
- CpawCTF2 (https://ctf2.cpaw.site/)
picoCTF (https://picoctf.org/)

常設CTFはたくさんネット上に転がっているので(Pwn系は特に多いです)、他にも見てみたい人はネットで調べてみると良いでしょう。

問題を解いていく中で、戦略に行き詰まることが必ずあるはずです。そんなときは迷わず解説を見ましょう。名が知られているコンテストでは、公式に解説がなくてもたいてい有志のかたが解法をブログなどに公開してくれています。この解説のことをWriteupといいます。Writeupを読むことで他の人がどのように解いたのか参考にできるので、自力で解けた問題でもWriteupを見てみるのも良いでしょう。

それでは、次の章から本編です。初心者がとっつきにくいPwnを除いたCrypto・Reversing・Web・Forensicsについて、例題を見ていきましょう。

3.6　Crypto編

Cryptoの問題では与えられた暗号を解いてflagを取得するのですが、この類の問題はセキュリティというよりは、数学や謎解きの性格が強いです。

早速ですが、例題を見てみましょう。

picoCTF 2021 - Mod 26

Cryptography can be easy, do you know what ROT13 is?

cvpbPGS{arkg_gvzr_V'yy_gel_2_ebhaqf_bs_ebg13_GYpXOHqX}

問題文に「ROT13を知っていますか？僕は知っています」的なことが書いてあるので、適当にROT13でググってみましょう。CTFではググる技術も問われます。

ROT13は非常に有名な暗号(?)で、平文の各アルファベットを後ろに13文字ぶん後ろにずらす、というものです。先ほど紹介したシーザー暗号のずらす個数を変えただけですね。

検索するとROT13を復号してくれるサイトが無限に出てくるので、適当なサイトで復号してみましょう。次の文字列になるはずです。

picoCTF{next_time_I'll_try_2_rounds_of_rot13_TLcKBUdK}

次の問題は、RSA暗号という有名な暗号を用いた問題です。RSA暗号についてはChito君が記事を書いてくれているようなので、彼に丸投げすることにします。興味のあるかたはご覧ください。

picoCTF 2021 - Mini RSA

What happens if you have a small exponent? There is a twist though, we padded the plaintext so that (M ** e) is just barely larger than N. Let's decrypt this:ciphertext

RSA暗号の体裁をとっていても、その値が脆弱では意味がありません。今回の場合、\( e=3 \)と小さいので、3乗根をとれば平文が手に入ってしまいます。この攻撃をLow Public-Exponent Attackといったりします。

import gmpy2
from Crypto.Util.number import *

N = int(input('N: '))
e = int(input('e: '))
c = int(input('c: '))

while True:
    m, exact = gmpy2.iroot(c, e)
    if exact:
        print(long_to_bytes(m))
        break
    c += N

\( c \)の3乗根が整数でとれるまで、\( c \)に\( N \)を足し続けています。RSA暗号の定義から\( c = m^{e} \bmod N \)なので、この3乗根が平文となります。これをバイト列と解釈して文字列に変換すると、

picoCTF{e_sh0u1d_b3_lArg3r_a166c1e3}

が手に入ります(運営側によってlArg3rの後の文字列はちょくちょく変更されます)。

他にも、Nが等しくeが異なる2つの公開鍵(e, N)が与えられれば、Common Modulus Attackで平文を入手することもできます。

3.7　Forensics編

Forensicsでは、与えられたファイル(画像、ディスクイメージ、etc.)に隠されたflagを見つけます。結構楽しいです。

簡単めな問題を見てみましょう。

picoCTF 2019 - extensions

This is a really weird text file TXT? Can you find the flag?

CTFでは問題名がヒントになっていることが多々あります。今回はextensions、つまり拡張子なので、拡張子をいじる問題だと推測できます。

では、このファイルの正しい形式は何でしょうか。実はそれが分かるコマンドがあります。

Linuxにはfileコマンドがあり、それを使うとファイル形式が表示されます。Windows10では、WSL(Windows Subsystem for Linux)を使えばWindows上でLinuxを使うことができます。

$ file ./flag.txt
flag.txt: PNG image data, 1697 x 608, 8-bit/color RGB, non-interlaced

これでファイルがpng形式だと分かりました。あとは拡張子を.pngに変更すると...

図3.1: 答え

この問題で使ったfileコマンドと、ファイル中の表示可能な文字列を出力するstringsコマンドはForensicsでは非常によく使われます。初手はこのコマンドを使うとよいでしょう。

3.8　Reversing編

Reversingでは基本的にアセンブリを読む作業が必要です。知識、経験、エスパーなどを駆使してプログラムの挙動をつかまないといけません。結構根性が要ります。

アセンブリの読み方は「アセンブリ入門」などと調べると結構な数がヒットするので、それを参考にするとよいでしょう(部誌で書くには締切が近すぎます)。ReversingやPwnは高度な知識が必要なので、後回しにしておくとよいのかもしれません。

それでは参考がてらに、アセンブリを使った問題をひとつ。

picoCTF 2019 - asm1

What does asm1(0x6fa) return? Submit the flag as a hexadecimal value (starting with '0x'). NOTE: Your submission for this question will NOT be in the normal flag format.

asm1:
    <+0>:   push   ebp
    <+1>:   mov    ebp,esp
    <+3>:   cmp    DWORD PTR [ebp+0x8],0x3a2
    <+10>:  jg     0x512 
    <+12>:  cmp    DWORD PTR [ebp+0x8],0x358
    <+19>:  jne    0x50a 
    <+21>:  mov    eax,DWORD PTR [ebp+0x8]
    <+24>:  add    eax,0x12
    <+27>:  jmp    0x529 
    <+29>:  mov    eax,DWORD PTR [ebp+0x8]
    <+32>:  sub    eax,0x12
    <+35>:  jmp    0x529 
    <+37>:  cmp    DWORD PTR [ebp+0x8],0x6fa
    <+44>:  jne    0x523 
    <+46>:  mov    eax,DWORD PTR [ebp+0x8]
    <+49>:  sub    eax,0x12
    <+52>:  jmp    0x529 
    <+54>:  mov    eax,DWORD PTR [ebp+0x8]
    <+57>:  add    eax,0x12
    <+60>:  pop    ebp
    <+61>:  ret

この関数では、アドレス[ebp+0x8]に引数が入っています。この引数をcmp命令で比較し、その直後のjgやjne命令で比較結果によって次に実行する命令にジャンプします。

行<+0>・<+1>はおまじないのようなものと思ってください。

<+3>で0x6faと0x3a2を比較します。0x6faのほうが大きいので(jg)、<+37>にジャンプします。

次に、<+37>で0x6faと0x6faを比較します。値が等しいので、ジャンプはせずそのまま次の行に移ります。

<+46>でeaxレジスタに値0x6faを入れています。その次の行<+49>でeaxレジスタの値を0x12だけ引いています。つまりこの演算の後、eaxレジスタの値は0x6e8になっています。

最後に、<+52>の処理で行<+60>にジャンプし、処理終了です。

関数の返り値はeaxレジスタに入れることになっているので、答えは0x6e8です。

3.9　Web編

プログラムを解読したり脆弱性を突いたりするReversingやPwnとは違い、Webでは文字通りWebページの脆弱性を突きます。このジャンルもPwn同様、難しい部類に入ります。

今回は割合に簡単な問題を紹介します。

picoCTF 2019 - where are the robots

Can you find the robots? https://jupiter.challenges.picoctf.org/problem/36474/ or http://jupiter.challenges.picoctf.org:36474

Webサーバを構築したことのあるかたは、問題文を読んでやるべきことが分かるかと思います。

robots.txtは、知られたくない情報を検索エンジンによって収集されないように、クローラー(Web上の画像や文書を取得しデータベース化するプログラム)を制御するためのファイルです。このファイルはサイトのトップディレクトリに置かれています。

なので、URL欄の末尾にrobots.txtを追加すると...

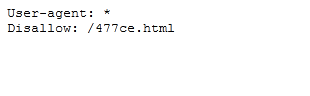
図3.2: robots.txt

このようにrobots.txtの中身が表示されてしまいます。そして、あからさまにhtmlファイルのリンクが書いてあるので、アクセスするとflagが手に入ります。

Web系の問題は学習難度が高く、なかなかとっつきにくいジャンルとなっています。

3.10　おわりに

今回はCTFの入門的問題ではどのようなものが出題されるか書きました。この記事がCTFを始める人に少しでも役に立てば嬉しいです。

それではよいCTFライフを。

第3章 CTF超入門

3.1 はじめに

3.2 注意

3.3 What's CTF

3.4 例題

3.5 CTFの学習方法

3.6 Crypto編