第8章 深層学習の基礎のキソ
72回生 吉岡拓真
直近の20年で最も大きなブレイクスルーと言っても過言ではないのが深層学習です。(クローズエンドな環境では)最強な深層学習。本記事ではその技術の基礎であるニューラルネットワークについて述べていきます。
8.1 単層・多層パーセプトロン
本節ではパーセプトロンというアルゴリズムについて説明します。かなり古いアルゴリズムですが、ニューラルネットワークへの導入として解説書などではよく用いられます。
パーセプトロンとは
本記事では2入力のパーセプトロンについて扱います。2入力のパーセプトロンは2つの入力を受け取り、1つの信号を出力する関数のことです。その出力は0か1のどちらかで、重みという値を入力に掛け合わせることでその入力の重要度を操作するのに使い、その掛け合わせた値の和w_1 x_1 + w_2 x_2(ここではw_1, w_2というのが重み)に対してバイアス(b)という値を加えたものに応じて0か1かを出力します。図示すると以下のようになります。
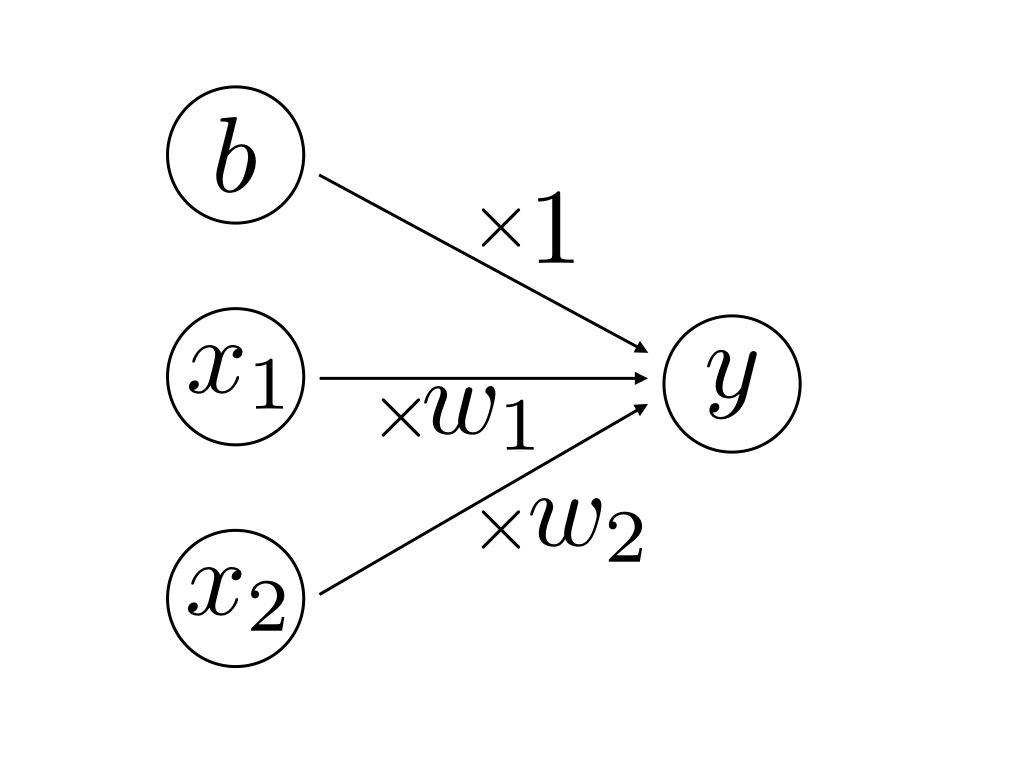
図8.1:
この図の「丸いもの」をユニットもしくはニューロンと呼びます。ここで、yは真ん中のユニットが出力する値で、以下のように定義します。
y = \begin{cases}
1 & (w_1 x_1 + w_2 x_2 + b > 0) \\
0 & (w_1 x_1 + w_2 x_2 + b \leq 0)
\end{cases}
重みの値が大きければ大きいほど、その重みが掛けられる入力の値は出力に影響をより与える、すなわち「重要度が高い」入力となります。
論理回路
2入力のパーセプトロンを用いて論理回路を実装していきます。使用言語はpythonです。
ANDゲート
ANDゲートは下の表のように、2つの値両方が1の時のみ1を出力するような回路です。また、下の表のような入力信号と出力信号の対応表を真理値表と呼びます。
表8.1: ANDゲートの真理値表
| x_1 | x_2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
これをパーセプトロンで実装します。w_1 = 0.5, \, w_2 = 0.5, \, b = -0.7というように重みとバイアスの値を決めるとその出力は上の真理値表を満たします。実際に計算してみてください。pythonでの実装は次のようになります。
リスト8.1: AND.py
m, n = list(map(int, input().split())) def AND(x1, x2): w1, w2, b = 0.5, 0.5, -0.7 t = w1 * x1 + w2 * x2 + b if t > 0: return 1 else: return 0 print(AND(m, n))
NAND, ORゲート
ANDゲートと同様にNANDゲートとORゲートを実装します。それぞれの真理値表は以下の通りです。
表8.2: NANDゲートの真理値表
| x_1 | x_2 | y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
表8.3: ORゲートの真理値表
| x_1 | x_2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
ちなみに「NAND」は「Not AND」を意味しているので出力される値はANDゲートと真逆です。この2つの論理回路もパーセプトロンで表現することができます。NANDゲートはw_1 = -0.5, \, w_2 = -0.5, \, b = 0.7というように、ORゲートはw_1 = 0.5, \, w_2 = 0.5, \, b = -0.2というように重みとバイアスの値を決めるとうまくいきます。実装は先ほどのANDゲートとさして変わらないので省略します。
XORゲート
XORゲートの真理値表は以下の通りです。
表8.4: XORゲートの真理値表
| x_1 | x_2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
しかしながら、これは今までのようにはいきません。重みやバイアスの値を上手に調整して実装しようとしてもこれは不可能です。「線形分離不可能」と言って、2次元平面の2点を直線で分離できないことを指す言葉なんですが、単層のパーセプトロンでは解決できない問題なんです。単層のパーセプトロンでは解決できないので、多層にして解決します。多層にすることで、単層では解決できなかった問題が解決できるようになる様子を見ていきましょう。
XORゲートは今までのAND・NAND・ORゲートを下の図のように組み合わせることで実装することができます。
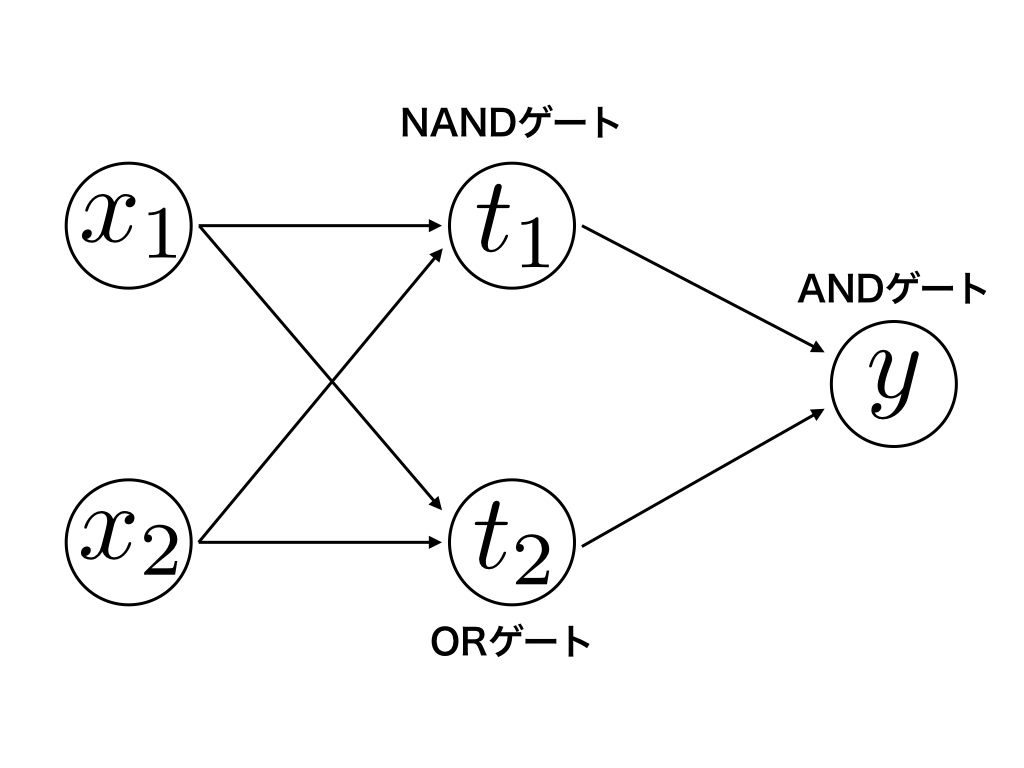
図8.2:
これを真理値表で表すと下の表のようになります。
表8.5: XORゲートの真理値表
| x_1 | x_2 | t_1 | t_2 | y |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
AND・NAND・ORゲートを介することでXORゲートを作成することができます。pythonでの実装は以下の通り。
リスト8.2: XOR.py
m, n = list(map(int, input().split())) def AND(x1, x2): w1, w2, b = 0.5, 0.5, -0.7 t = w1 * x1 + w2 * x2 + b if t > 0: return 1 else: return 0 def NAND(x1, x2): w1, w2, b = -0.5, -0.5, 0.7 t = w1 * x1 + w2 * x2 + b if t > 0: return 1 else: return 0 def OR(x1, x2): w1, w2, b = 0.5, 0.5, -0.2 t = w1 * x1 + w2 * x2 + b if t > 0: return 1 else: return 0 def XOR(x1, x2): t1 = NAND(x1, x2) t2 = OR(x1, x2) out = AND(t1, t2) return out print(XOR(m, n))
XORゲートを通して、多層にすることの「良さ」を述べてきました。パーセプトロンは深層学習の本当に基礎なのでしっかり押さえておきましょう。
余談
ぶっちゃけXORゲートは3行で実装できます。
リスト8.3: _XOR.py
n, m = list(map(int, input().split())) if (n or m) and not(n and m): print(1) else: print(0)
8.2 順伝播型ネットワーク
本節では順伝播型ネットワークについて解説します。順伝播型ネットワークは層状に並べられたユニットが、隣り合った層のユニットと結合し1方向に情報を伝播させていくネットワークで、ニューラルネットワークの中でもっとも基本的なものです。
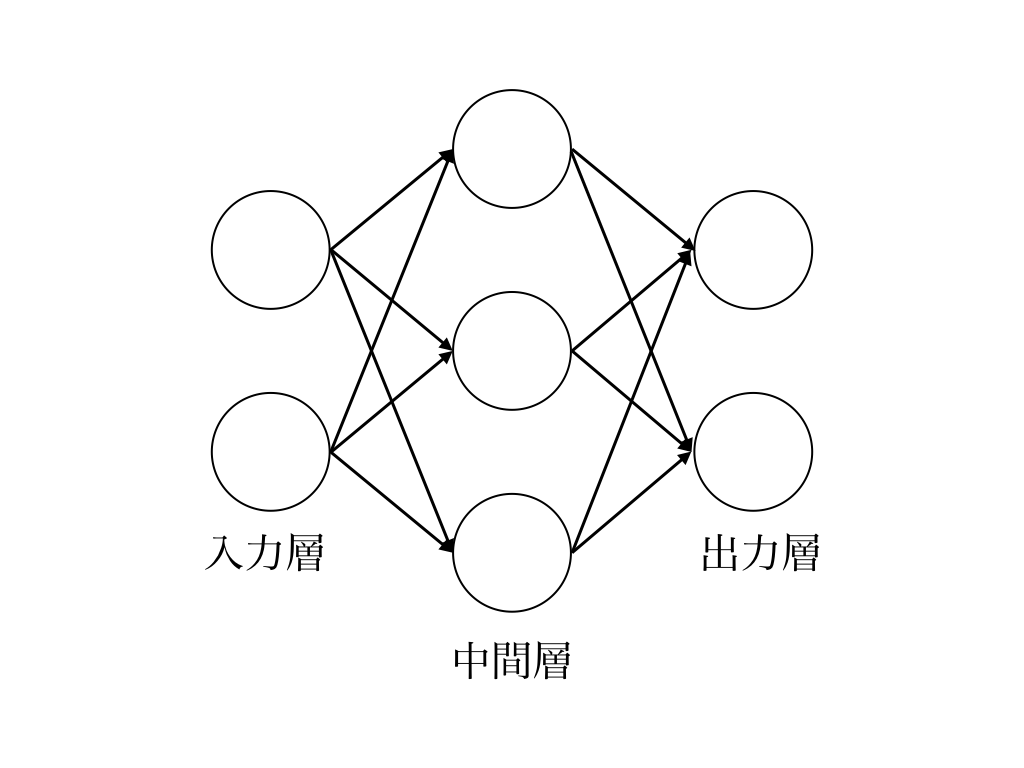
図8.3:
上の図において、一番左の層を入力層、真ん中の層を中間層、右の層を出力層と呼びます。
ユニットの構造
ネットワークを構成するユニットは複数の入力を受け取り1つの値を出力します。次の図のようにx_1 ~ x_4までの4つの入力がある場合、ユニットが受け取る総入力uは
u = w_1 x_1 + w_2 x_2 + w_3 x_3 + w_4 x_4 + b
となります。図ではバイアスを省略しています。ユニットの出力zは活性化関数と呼ばれる関数fのuに対する出力となります。
z = f(u)
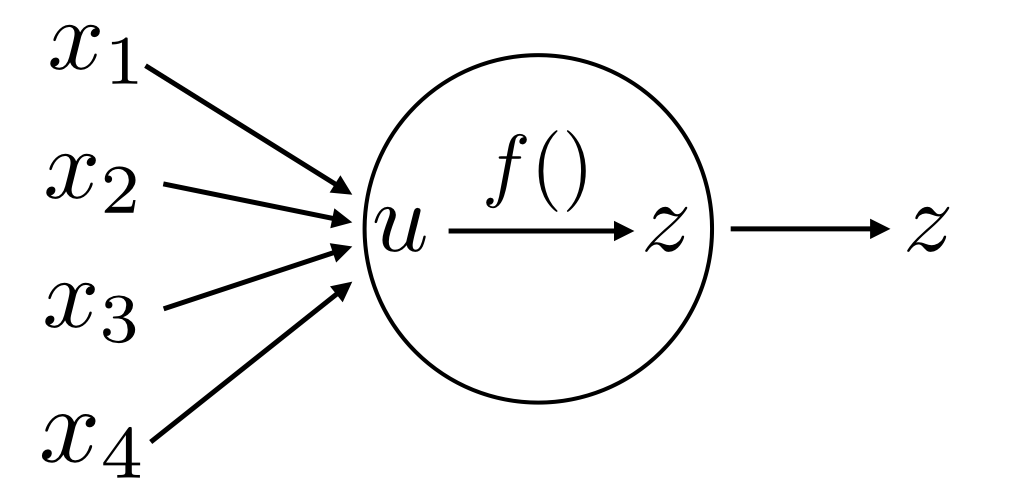
図8.4:
順伝播型ネットワークはこのユニットを並べた層同士が次の図のように結合し情報を受け渡していきます。
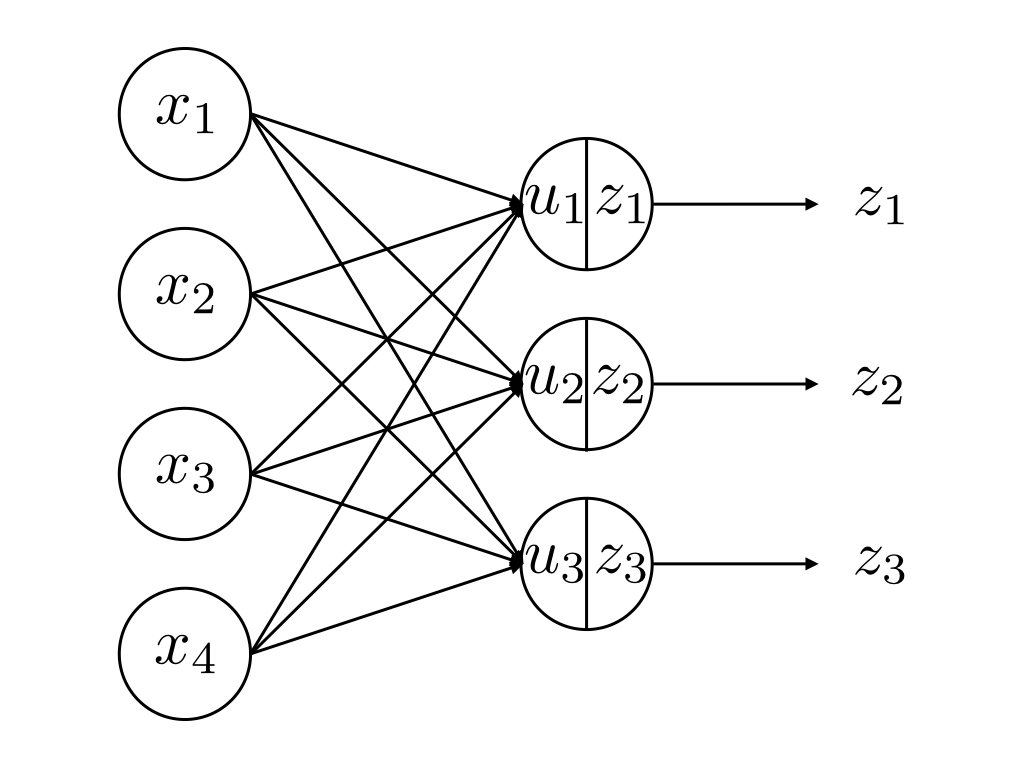
図8.5:
一層目のユニット数をI、二層目(z_jを出力している層)のユニット数をJとすると、各ユニットの入力と出力を一般化すると以下のようになります。(i = 1,\, 2,\, \ldots \, I ,\,\, j = 1,\, 2,\, \ldots \, J)
\begin{aligned}
u_j &= \sum_{i}^I w_{ji} x_i + b_j \\
z_j &= f(u_j)
\end{aligned}
ここではi番目のユニットとj番目のユニットの間の結合における重みをw_{ji}としています。これを行列で表すと以下の通りです。
\begin{aligned}
\mathbf{u} &= \mathbf{W} \mathbf{x} + \mathbf{b} \\
\mathbf{z} &= \mathbf{f}(\mathbf{u})
\end{aligned}
ただし、各行列・ベクトルを次のように定義しています。
\begin{aligned}
& \mathbf{u} = \left(
\begin{array}{c}
u_1 \\
u_2 \\
\vdots \\
u_J
\end{array}
\right)
,\,
\mathbf{W} = \left(
\begin{array}{cccc}
w_{11} & w_{12} & \ldots & w_{1I} \\
w_{21} & w_{22} & \ldots & w_{2I} \\
\vdots & \vdots & \ddots & \vdots \\
w_{J1} & w_{J2} & \ldots & w_{JI}
\end{array}
\right)
,\,
\mathbf{x} = \left(
\begin{array}{c}
x_1 \\
x_2 \\
\vdots \\
x_I
\end{array}
\right)
,\, \\ &
\mathbf{b} = \left(
\begin{array}{c}
b_1 \\
b_2 \\
\vdots \\
b_J
\end{array}
\right)
,\,
\mathbf{z} = \left(
\begin{array}{c}
z_1 \\
z_2 \\
\vdots \\
z_J
\end{array}
\right)
,\,
\mathbf{f}(\mathbf{u}) = \left(
\begin{array}{c}
f(u_1) \\
f(u_2) \\
\vdots \\
f(u_J)
\end{array}
\right)
\end{aligned}
活性化関数の種類
先ほど登場した活性化関数の中で代表的なものとその実装を紹介します。
Sigmoid関数
Logistic関数とも呼ばれます。定義は次の通り。
f(x) = \frac{1}{1 + \mathrm{e}^{-x}}
この関数は入力の絶対値が大きな値であると出力は一定の値に近づき、この関数の値域は(0, 1)です。また全ての実数xで微分可能であることが特徴です。pythonで実装すると次のようになります。
リスト8.4: Sigmoid.py
def sigmoid(x): return 1 / (1 + np.exp(-x))
入出力は省略しました。これを実行すると、例えば、入力1に対しては0.7310585786300049を出力し、入力5に対しては0.9933071490757153を出力します。
双曲線正接関数
f(x) = \tanh (x)
で定義される関数です。双曲線関数の様々な性質にはここでは触れませんが、この関数は値域が(-1, 1)でシグモイド関数と似た性質を持っています。numpyの関数に存在しているので実装は省略します。
ReLU関数(正規化線形関数)
f(x) = \max (x, 0)
で定義される関数で、非常に単純なのでpythonでの実装は省略します。この関数はその単純さゆえに計算量が非常に少なく、また学習がとても早く進むため、とてもよく使われる活性化関数です。
恒等関数
f(x) = x
で定義される関数。ここで紹介する活性化関数の中で唯一の線形関数です。出力層で使われることがあります。
Softmax関数
Softmax関数も出力層で使われます。出力層のユニット数をKとし、出力層のうちk番目のユニットの出力を
z_k = \frac{\exp(u_k)}{\sum_{j}^{K} \exp(u_j)}
とします。この関数をSoftmax関数と呼び、\sum_{k}^{K} z_k = 1が成り立つという特徴があります。そのため、手書き文字の認識などの多クラス分類によく使用されます。出力される値の和が常に1なら、出力をデータが各クラスに分類される確率として捉えることができるからです。例えばz_k = 0.53ならk番目のクラスに分類される確率が53%であると解釈できるということです。
Softmax関数の実装
Softmax関数を愚直に実装すると次のようになります。
リスト8.5: _Softmax.py
def _Softmax(x): exp_x = np.exp(x) sum_exp = np.sum(exp_x) y = exp_x / sum_exp return y
しかしこれでは簡単にオーバーフローを起こしてしまうので全く使えません。そこで次の式を参考にこのコードを改善します。
z_k = \frac{\exp(u_k)}{\sum_{j}^{K} \exp(u_j)} = \frac{C \exp(u_k)}{C \sum_{j}^{K} \exp(u_j)}
= \frac{\exp(u_k + \log C)}{\sum_{j}^{K} \exp(u_j + \log C)}
\frac{\exp(u_k + C')}{\sum_{j}^{K} \exp(u_j + C')}
この式においてCは任意の定数で、\log CをC'と置き換えています。C'の値をうまく取ってやることでオーバーフローを防ぐことができます。具体的には、u_j(j = 1,\, 2,\, \ldots \, K)の最大値をC'に代入するとうまくいきます。それを踏まえてSoftmax関数の実装すると次のようになります。
リスト8.6: Softmax.py
def softmax(x): c = np.max(x) exp_a = np.exp(x - c) sum_exp = np.sum(exp_a) y = exp_a / sum_exp return y
線形関数と非線形関数
線形関数というのはf(x) = a x\,(aは定数)のように出力が入力の定数倍になるような関数のことで、活性化関数では線形関数を使用することに意味はありません。なぜなら複数の層に渡り活性化関数を通した変換を行なっても、例えば3層の場合では、f(f(f(x))) = a \times a \times a \times xとなりますが、この計算はa^3 = bとした時、h(x) = b xという計算を行うことと等しいからです。
8.3 勾配法
誤差関数
損失関数とも呼ばれる関数で、現在のネットワークが教師データに対してどれだけ適合していないかという指標で、ネットワークの性能の「悪さ」を表します。
2乗誤差
ネットワークの出力をy_k、教師データをt_kとすると、2乗誤差は以下のように計算されます。
E = \frac{1}{2} \sum_k (y_k - t_k)^2
この\frac{1}{2}は微分した時に次数と打ち消しあわせるためにあります。実装は以下の通り。
リスト8.7: mean_squared.py
def mean_squared(y, t): return 0.5 * np.sum( (y - t)*2 )
交差エントロピー
先程と同様に、ネットワークの出力をy_k、教師データをt_kとします。
E = - \sum_k t_k \log y_k
ただし、ここでのt_kは正解ラベルを持つインデックスのみ1でその他が0であるとします(これをone-hot表現と呼びます)
愚直に誤差を計算すると数値の積になる誤差を和の形で表すために対数を取っています。また、出力と教師データの差異が大きいほどこの値Eは大きくなります。つまり、ネットワークの目標はEをできるだけ小さい値になるようにすることです。この状況は先ほどの式の左辺にマイナスが付いていることによって生み出されています。実装は以下の通り。
リスト8.8: cross_entropy.py
def cross_entropy return -np.sum( t * np.log(y + 1e-7) )
実装において、np.logを計算する際に微小な値を加えることで、np.log(0)という計算が発生することを防いでいます。np.log(0)は負の無限大を表す-infを出力してしまうのでこの処理が必要となります。
バッチ学習
ここからは学習の方法をいくつか紹介します。学習の目的は誤差関数E(\mathbf{w})(全ての層の間の重みとバイアスの全てを成分にもつベクトルを\mathbf{w}と定義します)の値を小さくするような重みを求めることです。一般的に、誤差関数は凸関数ではないので誤差関数が最小値をとる解を求めることは不可能です。ですが、誤差関数の局所的な最小解を求めることはできます。最小値を与える重みでなくとも、十分に小さい値を与えるならば問題を解決する分には事足りるということです。
何らかの初期値をスタートとして、重みwを繰り返し更新することでそのような解を求めることができます。ここで勾配を利用します。勾配とは以下のようなベクトルです。
\nabla E = \frac{\partial E(\mathbf{w})}{\partial \mathbf{w} } = \left(
\begin{array}{c}
\displaystyle \frac{\partial E(\mathbf{w})}{\partial w_1 } \\ \\
\displaystyle \frac{\partial E(\mathbf{w})}{\partial w_2 } \\ \\
\vdots \\ \\
\displaystyle \frac{\partial E(\mathbf{w})}{\partial w_m }
\end{array}
\right)
ここで、\mathbf{w}の要素数をmとしました。この勾配を利用して重みを更新していきます。更新する前の重みを\mathbf{w}、更新した後の重みを\mathbf{w'}とすると
\mathbf{w} \gets \mathbf{w} - \eta \nabla E
というように重みを更新します。\etaは重みの更新する量を決める値で学習係数と呼ばれます。この際、訓練データの数をNとした時、最小化しようとしている誤差関数は全ての訓練データn = 1, \, 2, \, \ldots \, Nに対して計算される誤差関数の和、すなわち、各データ1つに対して計算される誤差E_n(\mathbf{w})の和で
E(\mathbf{w}) = \sum_n^N E_n(\mathbf{w})
として与えられます。バッチ学習は全てのデータについて毎回誤差関数を求めて足し合わせているため、計算コストが非常に高く、また最小化しようとする誤差関数常にE(\mathbf{w})であるので、望まない局所解、つまり誤差関数の値がそれほど小さいわけではない局所解にトラップしてしまった時に抜け出せないという欠点を抱えています。
確率的勾配降下法
確率的勾配降下法は先ほどのバッチ学習の欠点を解消したものです。バッチ学習が訓練データ1つ1つの誤差関数(E_n(\mathbf{w}))の和E(\mathbf{w})の勾配\nabla Eで重みを更新するのに対して、確率的勾配降下法は訓練データから1つのデータを取り出し、そのデータの誤差関数(E_n(\mathbf{w}))の勾配\nabla E_nによって以下のように重みを更新します。
\mathbf{w} \gets \mathbf{w} - \eta \nabla E_n
確率的勾配降下法はバッチ学習の欠点を解消したものではありますが欠点はあります。まず、ランダムにデータを取り出しているため最短で最適解にたどり着くわけではありません。ただ、1回あたりの計算量が少ないので結果的に早い場合もあります。次に、データを1つずつ利用しているので、異常なデータ(いわゆる外れ値)に引きずられやすいです。さらに学習係数の設定に失敗すると劇的に悪化する場合があります。
ミニバッチ学習
ミニバッチ学習はバッチ学習と確率的勾配降下法の「良いとこどり」をしたような学習アルゴリズムです。確率的勾配降下法ではデータ1つずつ重みを更新していましたが、ここではいくつかのデータの集合(これをミニバッチと呼ぶ)の単位で重みを更新していきます。具体的には以下のように重みを更新していきます。
\mathbf{w} \gets \mathbf{w} - \eta \frac{1}{N} \sum_n^{N} \nabla E_n
ここで、Nはミニバッチとして取り出したデータの数を表しています。ミニバッチのサイズは10~100あたりにするのが一般的です。
8.4 誤差逆伝播法
前節で誤差関数とそれを最小化する手法を紹介しました。その更新式をそのまま実装しても当然求めたい重みは求まりますが、何度も何度も誤差関数を微分して重みを更新するという計算を繰り返すのは計算コストがかかります。そこで誤差逆伝播法の出番です。愚直に微分していては重みの成分1つごとに微分する必要があります。それに対して、誤差逆伝播法では出力層に近い層から順に重みの微分を求めて行くのですが、その際に前回の計算結果を利用するので計算コストがあまりかからないというわけです。抽象的な話になってしまいましたので、具体的な説明をします。ここからは数式ばかり登場します。
連鎖律
微分の連鎖律について記述します。まず、1変数関数f,\, gについて、以下が成立します。
\frac{df}{dx} = \frac{df}{dg} \frac{dg}{dx}
次に多変数関数fと1変数関数gについて、以下が成立します。
\frac{\partial f}{\partial x} = \sum_k \frac{\partial f}{\partial g} \frac{\partial g}{\partial x}
証明は省きます(筆者は連鎖律の証明を理解していません。精進不足で申し訳ありません)
成分ごとの計算
最終的には行列で計算を行いますが、説明の準備として成分ごとの計算について記述します。
まず、誤差関数をEとした時、\displaystyle \frac{\partial E}{\partial w_{ji}^{(l)}}について考えます。記号の右肩についている(l)は第l層の重みであることを表します。u_j^{(l)}をw_{ji}^{(l)}についての式と考えて、先ほどの連鎖律から
\frac{\partial E}{\partial w_{ji}^{(l)}} = \frac{\partial E}{\partial u_{j}^{(l)}} \frac{\partial u_{j}^{(l)}}{\partial w_{ji}^{(l)}}
が成り立ちます。次にこの式の右辺の左側部分から考えていきます。
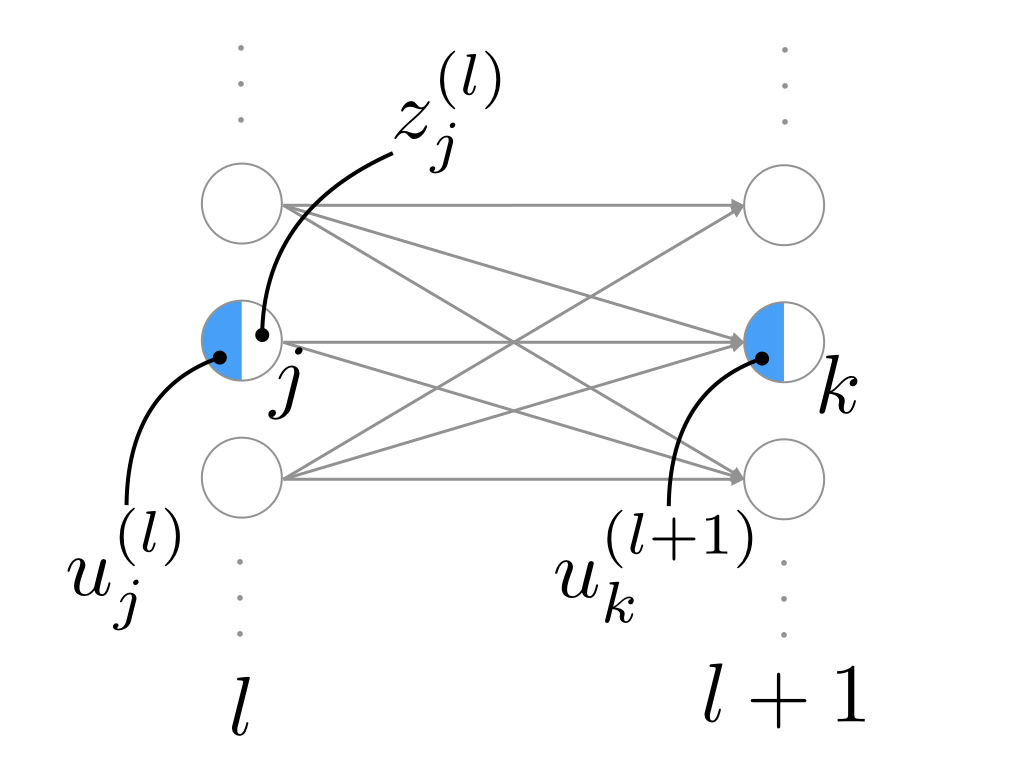
図8.6:
上の図のように、u_j^{(l)}はz_j^{(l)}を通してu_k^{(l+1)}に影響を与えます。したがって、
\frac{\partial E}{\partial u_{j}^{(l)}} = \sum_k \frac{\partial E}{\partial u_{k}^{(l+1)}} \frac{\partial u_{k}^{(l+1)}}{\partial u_{j}^{(l)}}
が成り立ちます。ここで、右辺にも\displaystyle \frac{\partial E}{\partial u_{k}^{(\cdot)}}と同じ形が現れていることに着目して、
\delta _j^{(l)} = \frac{\partial E}{\partial u_j^{(l)}}
と定義します。すると先ほどの式は
\delta _j^{(l)} = \sum_k \delta _k^{(l+1)} \frac{\partial u_{k}^{(l+1)}}{\partial u_{j}^{(l)}}
と書き直すことができます。さらに、u_{k}^{(l+1)} = \sum_m w_{km}^{(l+1)} z_m^{(l)} = \sum_m w_{km}^{(l+1)} f(u_m^{(l)})なので\displaystyle \frac{\partial u_{k}^{(l+1)}}{\partial u_{j}^{(l)}} = w_{kj}^{(l+1)} f'(u_j^{(l)})であるから、さらに
\delta _j^{(l)} = \sum_k \delta _k^{(l+1)} w_{kj}^{(l+1)} f'(u_j^{(l)})
と書き直せます。次に\displaystyle \frac{\partial u_j^{(l)}}{\partial w_{ji}^{(l)}}について考えます。

図8.7:
上の図のように、u_j^{(l)}はz_i^{(l-1)} w_{ji}^{(l)}\,\,(i = 1,\,2\,\ldots)の和として表せます。すなわち
u_j^{(l)} = \sum_i z_i^{(l-1)} w_{ji}^{(l)}
であるので、容易に
\frac{\partial u_j^{(l)}}{\partial w_{ji}^{(l)}} = z_i^{(l-1)}
と求まります。ここで初めの式に戻ると
\frac{\partial E}{\partial w_{ji}^{(l)}} = \delta _j^{(l)} z_i^{(l-1)}
これが求める微分です。この式を見ると、微分がただの積で表せています。さらに、\deltaは先ほどの式のように、繰り返し計算することができるので計算量コストを抑えることができます。
また、\deltaを求める際、最後の出力層(これを第L層とします)における\delta _k^{(L)}が必要になります。ですがこれは
\delta _k^{(L)} = \frac{\partial E}{\partial u_k^{(L)}}
と容易に計算することができます。交差エントロピーを誤差関数とし、出力層の活性化関数をSoftmax関数にした場合、出力層における\deltaは
\delta _k^{(L)} = - \frac{\partial \sum_m t_m \log y_m}{\partial u_k^{(L)}}
= - \frac{\partial \sum_m t_m \frac{\exp{u_m^{(L)}}}{\sum_i \exp{u_i^{(L)}}}}{\partial u_k^{(L)}}
= \ldots = y_k - t_k
途中計算は省略しました。やるだけなので頑張ってください。
行列による計算
先ほどの成分計算を行列に計算に当てはめます。重みw_{ji}(ただしここではバイアスを含めない)(j,i)要素にもつ行列を\mathbf{W}、ユニットjのバイアスをj番目の要素にもつベクトルを\mathbf{b}と表します。
入力されたデータを\mathbf{X}、この入力における第l層のユニットに対する総入力を\mathbf{U}^{(l)}、この総入力を活性化関数に通した出力を並べたベクトルを\mathbf{Z}^{(l)}とします。このとき、\mathbf{Z}^{(1)} = \mathbf{X}として、順伝播計算は以下のようになります。
\begin{aligned}
& \mathbf{U}^{(l)} = \mathbf{W}^{(l)} \mathbf{Z}^{(l-1)} + \mathbf{b}^{(l)} \\
& \mathbf{Z}^{(l)} = f^{(l)}(\mathbf{U}^{(l)})
\end{aligned}
f^{(l)}(\cdot)は行列の各成分に活性化関数を適応して、元の行列と同じ形の行列を出力するものとします。これらは2節で登場した式を行列で表したという理解で良いです。
さて、次に逆伝播の計算について考えます。前節の\delta _j^{(l)}を要素にもつ行列を\Delta ^{(l)}とします。\Delta ^{(l)}の各列は各ミニバッチに対応しています。逆伝播の計算は以下のようになります。
\Delta ^{(l)} = f^{(l)\prime}(\mathbf{U}^{(l)}) \odot (\mathbf{W}^{(l+1) \mathrm{T}} \Delta ^{(l+1)})
ここで、\odotという記号は行列の成分ごとの積を意味します。例を挙げると、A = {a_{ij}},\,B = {b_{ij}}について、A \odot Bの(i, j)成分はa_{ij} b_{ij}となります。出力層を第L層とすると、
\Delta ^{(L)} = \mathbf{Y} - \mathbf{T}
ただし、\mathbf{Y}は\mathbf{X}に対する出力\mathbf{Y}で、\mathbf{T}は目標となる出力です。
最後に\Delta ^{(l)}を用いた重みの更新式で勾配を計算します。重みw_{ji}^{(l)}についての誤差関数\sum_k^{N} E_n{\mathbf{W}}の微分を第(j, i)成分に持つ行列を\mathbf{W}^{(l)\prime}、バイアスb_j^{(l)}についての微分を第j成分に持つベクトルを\mathbf{b}^{(l)\prime}とします。するとこれらは次のように計算できます。
\begin{aligned}
& \mathbf{W}^{(l)\prime} = \Delta ^{(l)} \mathbf{Z}^{(l-1)\mathrm{T}} \\
& \mathbf{b}^{(l)\prime} = \Delta ^{(l)}
\end{aligned}
この2つを用いると、重みは以下のように更新できます。
\begin{aligned}
& \mathbf{W}^{(l)} \gets \mathbf{W}^{(l)} - \eta \mathbf{W}^{(l)\prime} \\
& \mathbf{b}^{(l)} \gets \mathbf{b}^{(l)} - \eta \mathbf{W}^{(l)\prime}
\end{aligned}
pythonで実装
さて、これまでのことを踏まえて実装していきます。今回はMNISTという手書き数字のデータセットを使います。このデータセットの読み込み方はここでは説明しませんが、ベンチマークとしてしばしば使われるものなのでインターネットにたくさん情報があります。MNISTは「手書き数字」なので0~9の10クラスの分類になります。この程度の分類問題だと深層にする意味が特にないので3層のパーセプトロンになります(複数層あるし実質深層ですって)(これは罠で本気の深層はもっと深イ)。中間層の活性化関数としてReLU関数を、出力層の活性化関数としてSoftmax関数を採用します。
誤差逆伝播法の説明では、一気にデルタを求めるという記述をしていましたが、実装では「活性化関数の順伝播・逆伝播計算を行うレイヤー」と「行列(出力と重みの計算)の順伝播・逆伝播計算を行うレイヤー」と役割を分けて考えます。つまり、ある層のデルタを求める時は活性化関数の逆伝播の計算を行ってから行列の逆伝播の計算をするということです。こういうように役割を分けるのには理由があります。活性化関数を変更した時にいちいちコードを書き直すのは手間がかかるので、活性化関数ごとのレイヤーを用意して、変更したい時はレイヤーを変更するだけでよくなるからです。さらに、逆伝播の計算途中の状態を取り出すことも容易にすることが可能になります。ちなみに計算グラフというもので誤差逆伝播法を考えると、このレイヤー分けはとても自然な流れで登場します。計算グラフについての説明は省きますが、今までのような数式だらけではないので分かりやすいと思います。
いよいよコードです。僕が1から作ったコードを載せることができれば良いのですが、「ゼロから作るDeep Learning」という本のコードがあまりに素晴らしすぎて超えることなどできないので、そのコードの実装する上で必要な部分だけ載せます。計算グラフについてはこの本によくまとめられています。レイヤー分けもこの本に書いてあるので読んでみてください。
まずは各関数です。ReLU関数に関しては処理が簡単なので、わざわざ関数としては実装していません。
リスト8.9: functions.py
import numpy as np def softmax(x): if x.ndim == 2: x = x.T x = x - np.max(x, axis=0) y = np.exp(x) / np.sum(np.exp(x), axis=0) return y.T x = x - np.max(x) return np.exp(x) / np.sum(np.exp(x)) def cross_entropy(y, t): if y.ndim == 1: t = t.reshape(1, t.size) y = y.reshape(1, y.size) if t.size == y.size: t = t.argmax(axis = 1) batch_size = y.shape[0] return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
Softmax関数のミニバッチ対応版
Softmax関数に少し追加している部分がありますね。これはミニバッチ学習に対応させたからです。ミニバッチを用いた場合、データはミニバッチのデータ数が行数、1つのデータが列ベクトルであるような行列です。変更を加える前のものは1つのデータに対する計算しかできません。変更後は複数のデータに対して同時に計算する機能が追加されているのでミニバッチ学習用の関数となっています。
次にレイヤーです。Affineというレイヤーが行列の演算を行います。ReluLayer、SoftmaxLossLayerはそれぞれ活性化関数の順伝播・逆伝播計算を行います。
リスト8.10: all_Layers.py
import numpy as np from functions import * class ReluLayer: def __init__(self): self.mask = None def forward(self, x): self.mask = (x <= 0) out = x.copy() out[self.mask] = 0 return out def backward(self, dout): dout[self.mask] = 0 dx = dout return dx class AffineLayer: def __init__(self, W, b): self.W = W self.b = b self.x = None self.dW = None self.db = None def forward(self, x): self.x = x out = np.dot(self.x, self.W) + self.b return out def backward(self, dout): dx = np.dot(dout, self.W.T) self.dW = np.dot(self.x.T, dout) self.db = np.sum(dout, axis = 0) return dx class SoftmaxLossLayer: def __init__(self): self.loss = None self.y = None self.t = None def forward(self, x, t): self.t = t self.y = softmax(x) self.loss = cross_entropy(self.y, self.t) return self.loss def backward(self, dout = 1): batch_size = self.t.shape[0] dx = (self.y - self.t) / batch_size return dx
そして逆伝播・順伝播を制御するコードです。順伝播計算を行った後、逆伝播を行い、重みを更新する量を求めます。地味ですが、OrderedDictが逆伝播するときに役立っています。
リスト8.11: network.py
import numpy as np from functions import * from all_layers import * from collections import OrderedDict class TwoLayerNet: def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01): self.params = {} self.params["W1"] = weight_init_std * np.random.randn(input_size, hidden_size) self.params["b1"] = np.zeros(hidden_size) self.params["W2"] = weight_init_std * np.random.randn(hidden_size, output_size) self.params["b2"] = np.zeros(output_size) self.layers = OrderedDict() self.layers["Affine1"] = AffineLayer(self.params["W1"], self.params["b1"]) self.layers["Relu1"] = ReluLayer() self.layers["Affine2"] = AffineLayer(self.params["W2"], self.params["b2"]) self.lastlayer = SoftmaxLossLayer() def predict(self, x): for layer in self.layers.values(): x = layer.forward(x) return x def loss(self, x, t): y = self.predict(x) return self.lastlayer.forward(y, t) def gradient(self, x, t): self.loss(x, t) dout = 1 dout = self.lastlayer.backward(dout) layers = list(self.layers.values()) layers.reverse() for layer in layers: dout = layer.backward(dout) grads = {} grads["W1"] = self.layers["Affine1"].dW grads["b1"] = self.layers["Affine1"].db grads["W2"] = self.layers["Affine2"].dW grads["b2"] = self.layers["Affine2"].db return grads
最後にこれらを利用してニューラルネットに学習させます。ここではミニバッチ学習を行っています。バッチサイズは100です。
リスト8.12: train.py
import numpy as np from mn.mnist import load_mnist from networks import TwoLayerNet (x_train, t_train), (x_test, t_test) = load_mnist(normalize = True, one_hot_label = True) network = TwoLayerNet(input_size = 784, hidden_size = 50, output_size = 10) iters_num = 10000 train_size = x_train.shape[0] batch_size = 100 learning_rate = 0.1 for i in range(iters_num): batch_mask = np.random.choice(train_size, batch_size) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] grad = network.gradient(x_batch, t_batch) for key in ("W1", "b1", "W2", "b2"): network.params[key] -= learning_rate * grad[key]
本当に学習できているのか確かめるために誤差関数の推移をグラフにしてみました。縦軸に誤差関数の値、横軸にミニバッチを利用して勾配を更新した回数を表示しています。
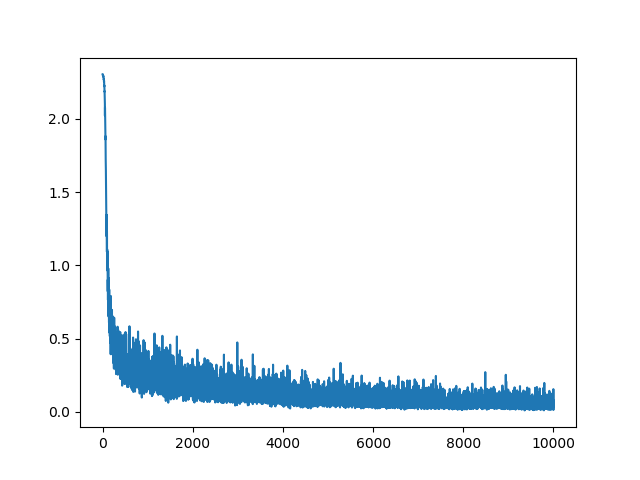
図8.8:
誤差関数が0に近づいて行っている様子が見て取れます。ここで、どれだけこのネットワークの精度が高いか調べてみましょう。network.pyにaccuracyという関数を追加します。これはどれだけ認識の精度が高いかを調べる関数です。
リスト8.13:
def accuracy(self, x, t): y = self.predict(x) y = np.argmax(y, axis = 1) if t.ndim != 1 : t = np.argmax(t, axis = 1) accuracy = np.sum(y == t) / float(x.shape[0]) return accuracy
これを利用して認識精度を計測します。ここでエポックという単位を導入します。1エポックとは学習において、訓練データを全て使い切った(とみなせる)時の回数に対応する数です。例えば、10000件のデータでミニバッチのデータ数が100ならば、10000 \div 100 = 100なので、100回が1エポックとなります。1エポック終えるごとに精度を調べることにします。train.pyの一部分を以下のように書き換えます。
リスト8.14:
#~省略~ train_acc_list = [] test_acc_list = [] iter_per_epoch = max(train_size / batch_size, 1) for i in range(iters_num): batch_mask = np.random.choice(train_size, batch_size) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] grad = network.gradient(x_batch, t_batch) for key in ("W1", "b1", "W2", "b2"): network.params[key] -= learning_rate * grad[key] if i % iter_per_epoch == 0: train_acc = network.accuracy(x_train, t_train) test_acc = network.accuracy(x_test, t_test) train_acc_list.append(train_acc) test_acc_list.append(test_acc) #~省略~
これをグラフに表すと以下のようになります。
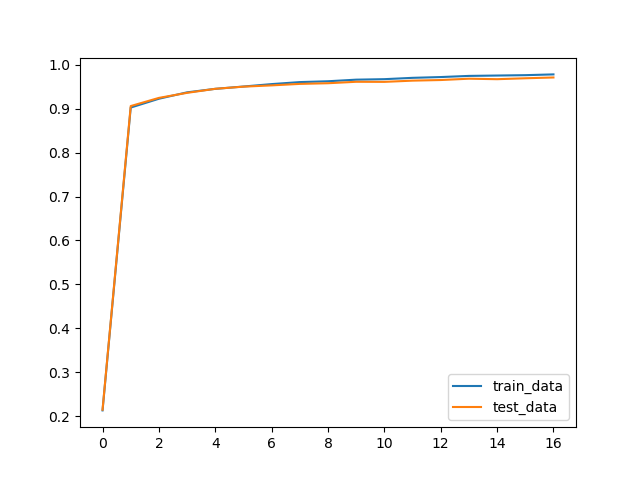
図8.9:
青色のグラフが訓練データにおける精度、オレンジ色がテストデータにおける精度となります。訓練データによって訓練されたネットワークがきちんと高い精度を出せていることがわかります。
8.5 あとがき
この記事に書いたことは深層学習というより、深層学習の元となっている技術の話です。3層のパーセプトロンや誤差逆伝播法は深層学習でなくとも使えるものですし、3層パーセプトロンは結構強力なものなので深層にするまでも無い場合もあります。また、数式で説明をしてきましたが、イメージが掴めないという方は「ゼロから作るDeep Learning」という本を読んでいただければなと思います。例えば誤差逆伝播法では、先ほど述べたとおり、計算グラフというもので解説されています。非常に分かりやすい考え方なので実装への導入も自然にできます。
後半はかなり飛ばして行きました。ソースコードに関しましては、ここまで読んでいただいた方には本当に申し訳ないと思います。自分なりのコードを書く段階で、「ゼロから作るDeep Learning」に掲載されていたコードがいかに洗練されているのかを痛感し、このような結果になりました。これは偏に僕の実力不足のせいです。申し訳ないと思うとともに、精進を誓う次第です。
最後になりましたが、ここまで読んでくださり本当にありがとうございます。本記事、ひいてはこの部誌を読み、我々NPCAや様々な技術に興味を持っていただければ幸いです。