第11章 グラフのおはなし
74回生 harady
こんにちは。74回生のharadyです。気づいたら高校生になってました。この前中学入学したんですが...。最近のマイブームは競技プログラミングです(通称競プロ)。競プロがどういうものかご存じで無い方は去年の物理好きさんの部誌を参考にしてください。今回は競プロにおけるグラフの問題について基礎的なことをまとめようと思います。自分自身も学習中なので、間違いは大目に見てください。
11.1 グラフの嬉しさ
現実世界の様々な事柄は、グラフを使って表現できることがあります。カーナビなどがいい例で、色々な場所とそれらを繋ぐ道路という構図はまさにグラフです。色々な場所をグラフに対応付けることで、ある地点からある地点への最短距離をグラフの最短経路問題に落とし込むことができます。
このようにグラフは様々な事象を表現するのに都合がよいので、グラフに関して多くのアルゴリズムやデータ構造が考案されています。
11.2 形式
今回の部誌では、競プロのグラフ問題で出てくる用語とデータ構造、アルゴリズムをC++による実装付きで書いていこうと思います。なおサンプルプログラムは全て動作を確認したわけでは無いので、自分で実装する時はGoogleなどで検索したり蟻本を読んだりする方が良いと思います。
11.3 用語集
計算量
プログラムの計算回数がある変数nに対してどれくらいの割合で変化するか、という数です。例えばfor (int i = 0;i < n;i++) for (int j = 0;j < n;j++) {hoge();}のようなコードの計算量はn^2に比例します。この場合計算量はO(n^2)と書きます。OはランダウのO記法です。一般的に、競技プログラミングにおいては計算回数が10^8を超えたあたりから制限時間に間に合うかが怪しくなり、10^9あたりからはお祈り次第になることが多いです。実行時間超過はTLE(Time Limit Exceeded)と呼ばれます。
蟻本
プログラミングコンテストチャレンジブックという本のことです。競技プログラミングで頻出の様々な話題を詳しく取り上げた、競プロerの聖書です。困ったらこの本を見ることで大体解決します。
グラフ(graph)
グラフと言っても、一般的に想像される棒グラフや折れ線グラフとは違います。グラフ理論におけるグラフは、頂点(node)と辺(edge)から構成されます。下の図のように、頂点と頂点の間を辺で結んだものがグラフです。
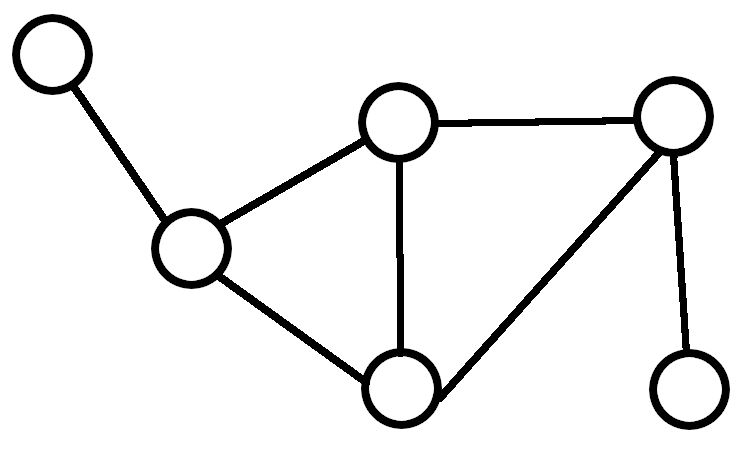
図: グラフ(graph)
重み(cost)
各辺について、その辺に付随する属性として重みを考えることがあります。これはカーナビで言うところの道路の長さにあたります。辺に重みがついたグラフのことを重み付きグラフ(weighted graph)といいます。
多重辺(multiple edges)
重複する複数の辺のことです。
ループ辺(loop)
ある頂点から出て同じ頂点に接続する辺のことです。
単純グラフ(simple graph)
多重辺とループ辺を持たないグラフです。
有向グラフ(directed graph)
辺に向きがあるグラフです。対立概念に無向グラフ(undirected graph)があります。競プロでは無向グラフを、任意の辺が結ぶ2頂点の間に互いに逆向きの辺を2本張った有向グラフと捉えることがあります。
閉路(cycle)
ある頂点から辺を辿ったときに、元の頂点に戻ってくるような道のりのことです。
連結グラフ(connected graph)
任意の2頂点間がいくつかの辺を通じて繋がっているグラフです。対立概念に非連結グラフ(disconnected graph)があります。ある頂点と別の頂点が繋がっていないグラフです。
木(tree)
閉路が無い連結グラフです。どの2頂点間にも辺が1本のみ存在します。木の一番上の頂点は根(root)です。各頂点は子となる頂点を持ちます。子を持たない頂点(末端の頂点)のことを葉(leaf)と呼びます。
森(forest)
閉路が無いグラフです。連結であるとは限りません。木は明らかに森です。
二部グラフ(bipartite graph)
隣接する頂点を塗り分けていったとき、2色で塗り分けることができるグラフです。
11.4 データ構造
データ構造とは、データの集まりを一定のルールに従って格納する為の形式のことです。
Union-Find木
よく考えたらUnion-Findをグラフ理論として紹介するのは謎なのですが、書いてしまったものを消すのも勿体無いので載せます...。
Union-Find木はグループ分けを管理するデータ構造です。競プロ以外の場ではdisjoint setと呼ばれることがあります。Union-Findではすべてのグループを木で管理します。
初期化
まずはn個の要素に対してn個の頂点を用意します。初めは辺がありません。
unite
ある2頂点を併合するときは、それぞれが含まれる木の片方の根からもう片方の根に辺を張ればよいです。
適当に繋げまくると木が偏り、探索に時間がかかる場合があります。そこで工夫をします。木の根にその木の深さをもたせておいて、併合する際には深さが浅い方から深い方へ繋ぐ、というのがよくあるやり方なのですが、木の深さよりその木に含まれる頂点の数のほうが必要とされる場面が多いので、今回はそちらで実装します。計算量は変わらないようです(理解していない)。
find
親を遡りながら根を探します。遡る途中で辿った頂点を根に繋ぎ直すことで高速化を図ります。uniteとfindの工夫をどっちもすることで計算量がO(α(n))になります。これはアッカーマン関数A(n,n)の逆関数です。アッカーマン関数は一瞬で膨大な数に膨れ上がることが知られており、これの逆関数なのでほぼO(1)と言って差し支えありません。
same
ある2頂点が同じグループに含まれる場合、その2頂点は必ず同一の木に含まれているので、2頂点の含まれる木の根が等しいかを判定すればよいです。
実装
UnionFind.cpp
class UnionFind { private: //parには親ノードの番号を格納する。その集合の根にあたるノードにはその集合の要素数*(-1)が入る(こうすることでpar[i]が負であるならばそのノードが根であることがわかる) vector<long long> par; public: //初期化するときは全てのノードが要素数1の集合であるとする UnionFind(int N) { par = vector<long long>(N, -1LL); } int find(int x); long long size(int x); void unite(int x, int y); bool same(int x, int y); }; //x番目のノードが属する集合の根を探す int UnionFind::find(int x) { //もしpar[x]が負ならx番目のノードは根なのでxを返す if (par[x] < 0) return x; //そうでないならx番目のノードの親についても同じことをしながらpar[x]を更新していく else return par[x] = find(par[x]); } long long UnionFind::size(int x) { return -par[find(x)]; } void UnionFind::unite(int x, int y) { //既に同じ集合に属しているならば繋げない if (same(x,y)) return; x = find(x); y = find(y); //大きい方に小さい方をくっ付ける if (size(x) < size(y)) swap(x, y); par[x] += par[y]; par[y] = x; } bool UnionFind::same(int x, int y) { x = find(x); y = find(y); return x == y; }
classで実装しています。UnionFind uf;uf = UnionFind(N)というように使います。割とトリッキーな実装だと思います。
find
findはx番目のノードが属する集合の根を探す関数です。自分の親の親の...が集合の根であるかを調べつつ、根が見つかったら探索中に通った全てのノードの親に根を設定します(つまり直接根に繋ぎます)。
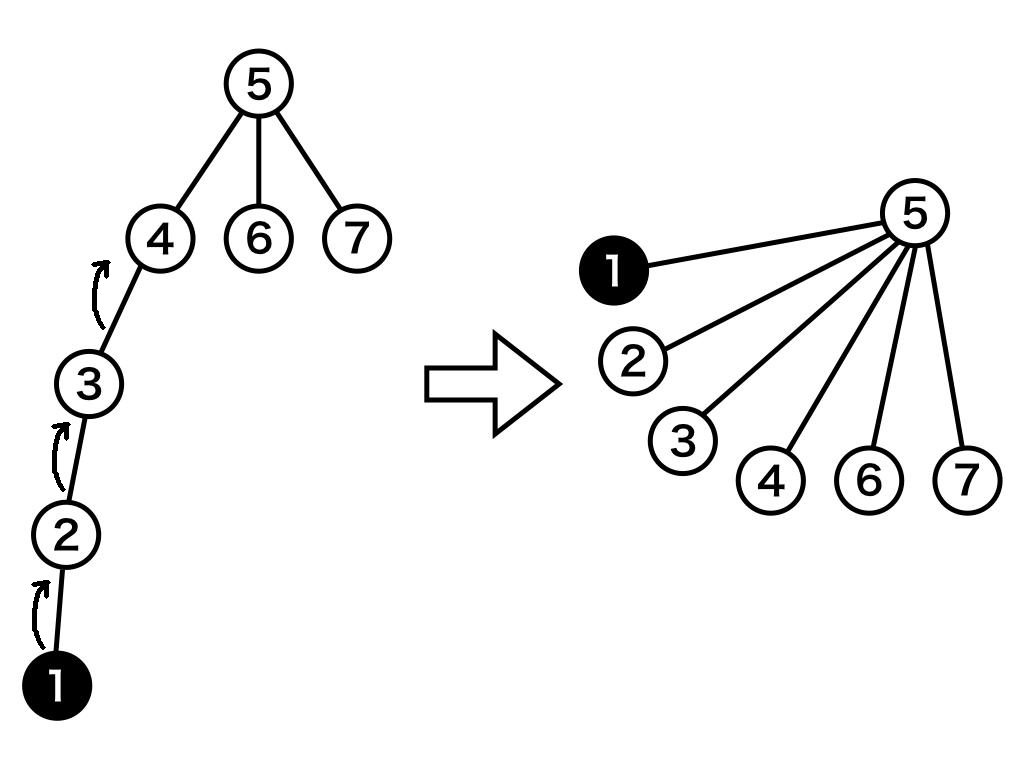
図: 直接根につなぎ直す
size
sizeはx番目のノードが属する集合の要素数を返す関数です。x番目のノードが属する集合の根のparの値に-1を掛けたものが要素数です。
unite
uniteはx番目のノードが属する集合とy番目のノードが属する集合を併合する関数です。x番目のノードの属する集合とy番目の集合の属する集合の要素数を比較して、要素数の多い方の根に要素数の少ない方の根を繋ぎます。
same
sameはx番目のノードとy番目のノードが同じ集合に属しているかを調べる関数です。x番目のノードの属する集合の親とy番目のノードの属する集合の親が等しければtrueを返し、異なればfalseを返します。
例題
問題
https://atcoder.jp/contests/abc120/tasks/abc120_d
実装例
https://atcoder.jp/contests/abc120/submissions/5119798
最小全域木(Minimum Spanning Tree)
最小全域木は、重みつきグラフの全ての頂点を結ぶ辺の集合の中で最も重みの総和が小さいものです。例えば、いくつかの都市の間に道を作って、最も短い距離の道で全ての都市を互いに行き来できるようにした時、それは最小全域木です。
最小全域木の求め方にはKruskal法とPrim法という有名なアルゴリズムがあります。ここではKruskal法の実装を行います。
概要
まずは全ての辺を重みで昇順にソートして、先頭から順にその辺を最小全域木に使うかを考えます。「A地点とB地点を繋ぐ辺について、既にAとBが連結であるならばその辺は使わず、連結でないならばその辺を使いAとBを連結にする」という判断を全ての辺に対して行うと最小全域木が出来上がります。「AとBが連結であるか」はUnion-Find木を使うことで判断できます。
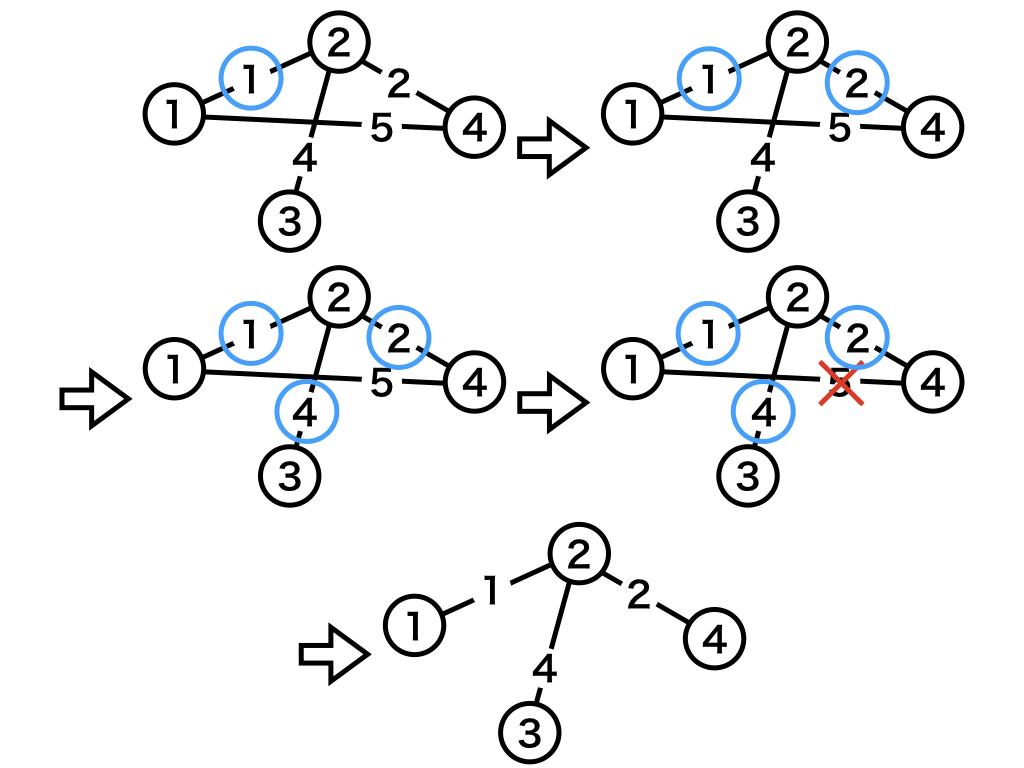
図: Kruskal法
実装(Kruskal法)
Kruskal.cpp
//(重み,(始点,終点)) typedef pair<long long, pair<int, int>> edge; class Kruskal { private: UnionFind *uf; //辺の集合 vector<edge> e; public: //mstに最小全域木を構成する辺をぶちこむ vector<edge> mst; Kruskal(int N) { uf = new UnionFind(N); } void add(int x, int y, long long z); void run(); }; void Kruskal::add(int x, int y, long long z) { e.push_back({ z,{x,y} }); } void Kruskal::run() { sort(e.begin(), e.end()); for (auto x : e) { //もし既に連結なら if (uf->same(x.second.first, x.second.second)) { //スルーして continue; } //そうでないなら else { //最小全域木にこの辺を追加して mst.push_back(x); //2地点をくっつける uf->unite(x.second.first, x.second.second); } } }
edgeは辺の重み、始点、終点を表します。
run
関数名は適当です。実行するとmstに最小全域木が格納されます。まず全ての辺を重みでソートして、上記の処理を行います。
ちなみにfor (auto x : e)はrange-based for文です。xにeの各要素が値渡しされます。xの中身を変更したければauto &xで参照渡しに出来ます。絶対に中身を変更したくない安全志向の人はconst auto &xとでもしたらいいと思います。
内部のUnion-Find木をポインタで保持しているので、メンバ関数へのアクセスはアロー演算子で行います。
Prim法
Prim法は、だんだん最小全域木を広げていくようなアルゴリズムです。初めに1つ適当な頂点を選び要素数1の集合とします。次に、その頂点からたどり着ける頂点の中で最も小さい重みで到達できる頂点を選んで集合に加え、行き先候補に新たに選んだ頂点から到達可能な頂点を加えます。これを繰り返して全ての頂点が集合に格納された時、その集合は最小全域木です。優先度付きキュー(priority queue)を使うことで全ての辺を重みが小さい順に保持することが可能です。
例題
問題
https://atcoder.jp/contests/arc076/tasks/arc076_b
実装例
https://atcoder.jp/contests/arc076/submissions/5175749
オーバーフローに親を殺された貴方へ
競プロをやっているとしばしば起きる悲劇がオーバーフローです。例えばint ans = 1'000'000'000'000'000;と書くとオーバーフローが発生します。AtCoderのコードテストで実行してみたところans = -1530494976と表示されました。この悲劇を回避するための一般的なテクニックとして#define int long longというものがあります。コードの頭にこれを書いておくことで、コード内のintという文字列が全てlong long(intより大きい値を持てる)に変換され、悲劇を回避することが出来ます。但しmain関数がlong longで宣言されているとコンパイラに怒られるので、signed main()と書けばよいです。
11.5 アルゴリズム集
今更ながらデータ構造とアルゴリズムを分けたのは間違いだった気がしていますが、気にせず書いていきます。
最短経路問題
やはりグラフと言えば一番有名なのは最短経路問題でしょう。ここでは3個の超有名アルゴリズムの解説をします。
Dijkstra法
読みは「ダイクストラ」です。「ディジェクストラ」ではありません。Dijkstra法はある点から他の全ての点への最短経路を求める大変高速なアルゴリズムです。priority_queueを採用した場合計算量はO((E+V) log V)です(Eは辺の数,Vは頂点の数)。グラフに重みが負な辺がない場合にこのアルゴリズムを適用することができます。
概要
到達可能な頂点と、その頂点へたどり着く為のコストの集合をQとします。はじめはQに出発点と出発時のコストを格納します。まず、出発点と繋がる頂点とその頂点にたどり着く為のコスト(つまり始点のコスト + (始点 -> その頂点)のコスト)をすべてQに格納します。Qの中でもっとも少ないコストでたどり着ける頂点を選び、その頂点のコストを確定します。次に選んだ頂点に繋がる頂点とその頂点にたどり着く為のコストをQに格納します。
これを繰り返しQが空集合になった時、全ての頂点への最短距離が求まっています。
参考
実装
綺麗な実装がしたいのですが、全然綺麗になりません...。
Dijkstra.cpp
#define INF 1e9+7 typedef struct { //私は誰ですか? int I; //どこからきたか。経路復元用 int from; int cost; //行き先,重み vector<pair<int,int>> to; } _node; bool operator > (const _node& a,const _node& b) { return a.cost > b.cost; } class Dijkstra { private: priority_queue<_node,vector<_node>,greater<_node>> pque; public: vector<_node> node; //要素数nで初期化 Dijkstra(int n) { node = vector<_node>(n); for (int i = 0;i < n;i++) { node[i].I = i; node[i].from = i; //はじめはcost無限大に設定 node[i].cost = INF; } } //辺を追加 void add(int start,int end,int cost); //実行。firstCostは開始時のコスト void dijkstra(int s,int firstCost = 0); }; void Dijkstra::add(int start,int end,int cost) { node[start].to.push_back({end,cost}); } void Dijkstra::dijkstra(int s,int firstCost = 0) { //スタート地点のコストを設定 node[s].cost = firstCost; //開始地点から到達可能な頂点をpriority_queueに入れる for (int i = 0;i < node[s].to.size();i++) { node[node[s].to[i].first].cost = node[s].to[i].second + node[s].cost; node[node[s].to[i].first].from = s; pque.push(node[node[s].to[i].first]); } //prioriry_queueが空だったら探索終了 while (!pque.empty()) { //更新候補 _node next = pque.top(); pque.pop(); //既にもっと小さいコストが確定しているならばスキップ if (next.cost > node[next.I].cost) continue; //更新を確定し、新たに行けるようになった頂点の更新候補をpriority_queueに入れる for (int i = 0;i < next.to.size();i++) { if (node[next.to[i].first].cost > next.cost + next.to[i].second) { node[next.to[i].first].cost = next.cost + next.to[i].second; node[next.to[i].first].from = next.I; pque.push(node[next.to[i].first]); } } } }
コメントを見たらわかると思います。「その時点で最もコストの小さい更新候補」はpriority_queueを使えばよいです。
Bellman-Ford法
Bellman-Ford法も用途はDijkstra法と変わりませんが、こちらはコストが負の辺があっても正しく動作しますし、コストの総和が負な閉路があった場合も検出可能です。また実装がシンプルです。探索の計算量はO(EV)です(Eは辺の本数,Vは頂点数)。
概要
初めに全ての頂点のコストをINFにし、スタート地点のコストをセットします。
次に全ての辺についてその辺を使うことで到達先のコストを減らせるかどうかを試します。これをn回繰り返すと、全ての(負閉路の一部でない)頂点の最小コストが求まります。n回目に更新がある場合、そのグラフにはコストの総和が負になる閉路(負閉路)が存在します。
実装
Bellman-Ford.cpp
#define INF 1e9+7; typedef struct { int from; int to; int cost; } Edge; class BellemanFord { private: vector<Edge> edge; public: vector<int> dist; BellemanFord(int n) { //初めは全ての頂点のコストがINFであるとする dist = vector<int>(n,INF); } void add(int from,int to,int cost) { edge.push_back({from,to,cost}); } bool bellemanford(int s,int n,int firstCost = 0) { dist[s] = firstCost; for (int i = 0;i < n;i++) { for (int j = 0;j < edge.size();j++) { //もしその辺を使ってコストを減らせるなら if (dist[edge[j].from] + edge[j].cost < dist[edge[j].to]) { //コストを更新 dist[edge[j].to] = dist[edge[j].from] + edge[j].cost; //もしn回目にも更新があったら負閉路が存在 if (i == n - 1) { return true; } } } } //もしreturnしていなければ負閉路は存在しない return false; } };
実装が単純なので、実行時間が気にならないのであればDijkstra法よりこちらのほうが手軽かもしれません。
Warshall–Floyd法
これは脳死実装です。Warshall-Floyd法を使うことで全ての2頂点間の最短距離が求まります。計算量はO(V^3)です。頂点が500個以上あるとTLEするかもしれません。
概要
2頂点(i,j)間の最短経路は、iからある頂点kへの最短経路とkからjへの最短経路を繋げたものだと考えることが出来ます(iとk、kとjが同じでも構わない)。よって、全てのi,j,kの組み合わせを調べれば任意の2頂点間の最短経路が求まります。i,j,kがそれぞれ頂点数だけ候補があるので、計算量はO(V^3)です。
実装
Warshall_Floyd.cpp
#define INF 1e9+7 class Warshall_Floyd { public: vector<vector<int>> d; void Warshall_Floyd(int n) { //ある頂点からある頂点はn^2通りある。初期化時はコスト無限大として良い d = vector<vector<int>>(n,vector<int>(n,INF)); } void add(int s,int e,int cost) { d[s][e] = cost; } bool warshall_floyd() { for (int k = 0;k < n;k++) { for (int i = 0;i < n;i++) { for (int j = 0;j < n;j++) { //k経由でi->j d[i][j] = min(d[i][j],d[i][k] + d[k][j]); } } } } }
これも実装はシンプルです。ちなみに、最近i,j,kの添字の順番を間違えても3回計算を繰り返せば正しい答えが出るという話が話題になりました。この記事に解説があります
https://qiita.com/tmaehara/items/f56be31bbb7a468a04ed
最大流問題
実は最大流問題は自分も使ったことがないので蟻本を写経しつつ解説します...。
最大流問題とは、各辺について通過できるコストの上限が決まっているような場面で頂点sから頂点tに最大でどれだけのコストを流せるか、ということを考える問題です。と言ってもこれだけではわかりにくいので例題を載せて解説します。
問題
ネットワーク上の2台のコンピュータs,tがあり、sからtにデータを送りたいとします。このネットワークには全部でN台のコンピュータがあり、いくつかのコンピュータの間は一方向性の通信ケーブルで接続されていて、それぞれ1秒間に通信できる最大のデータ量が決まっています。他のコンピュータが通信を行っていない時、sからtへ1秒間で最大どれだけのデータを送信することができるでしょうか。
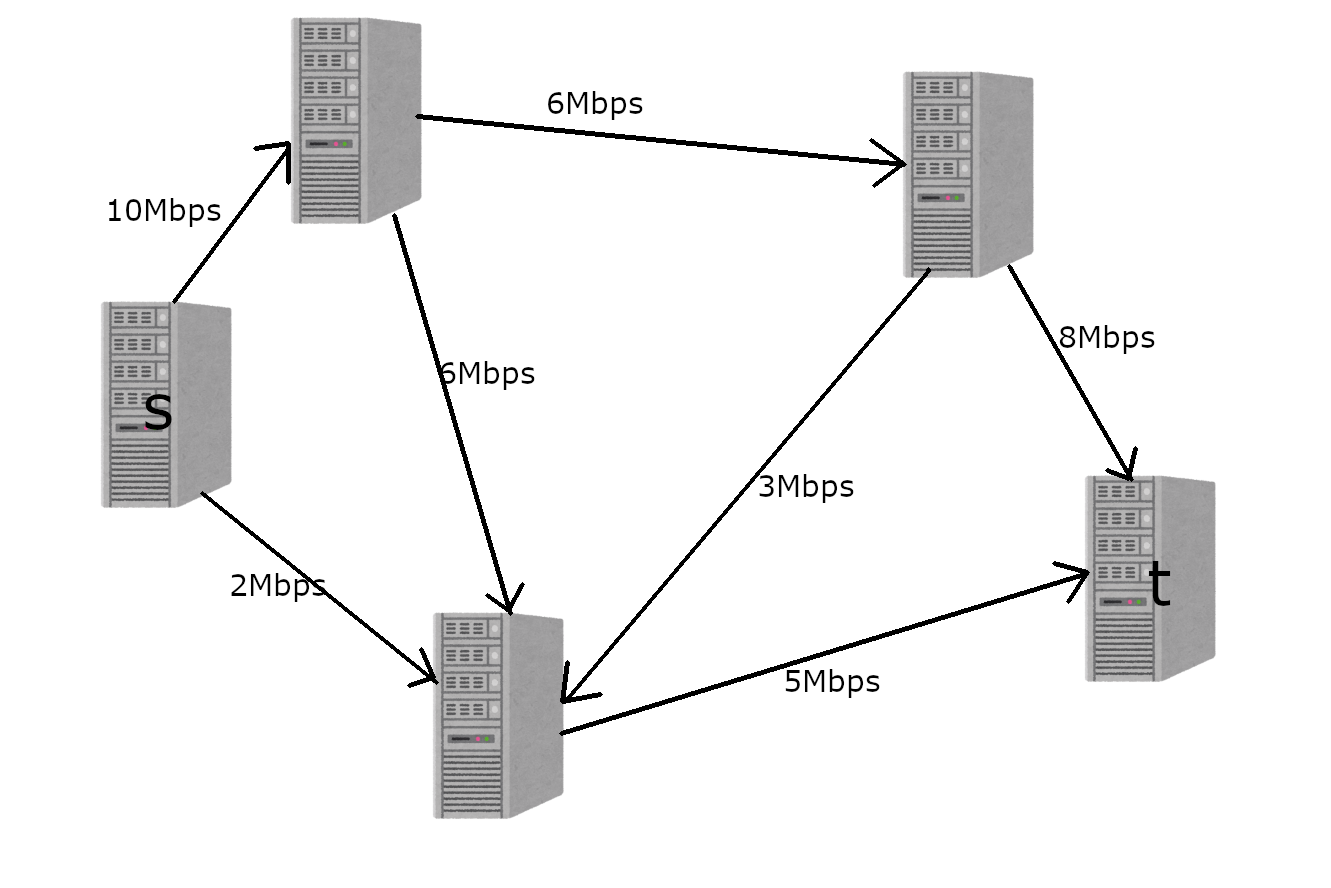
解き方
各辺の最大流量をc(e)、実際の流量をf(e)とします。まず、次のような単純な貪欲法を考えてみます。
- f(e)<c(e)であるcのみを用いたsからtへのパスを見つける
- そのようなパスが存在しなければ終了。パスが存在したら、そのパスに沿って目一杯流して1に戻る
この貪欲を行うと次のようになります。
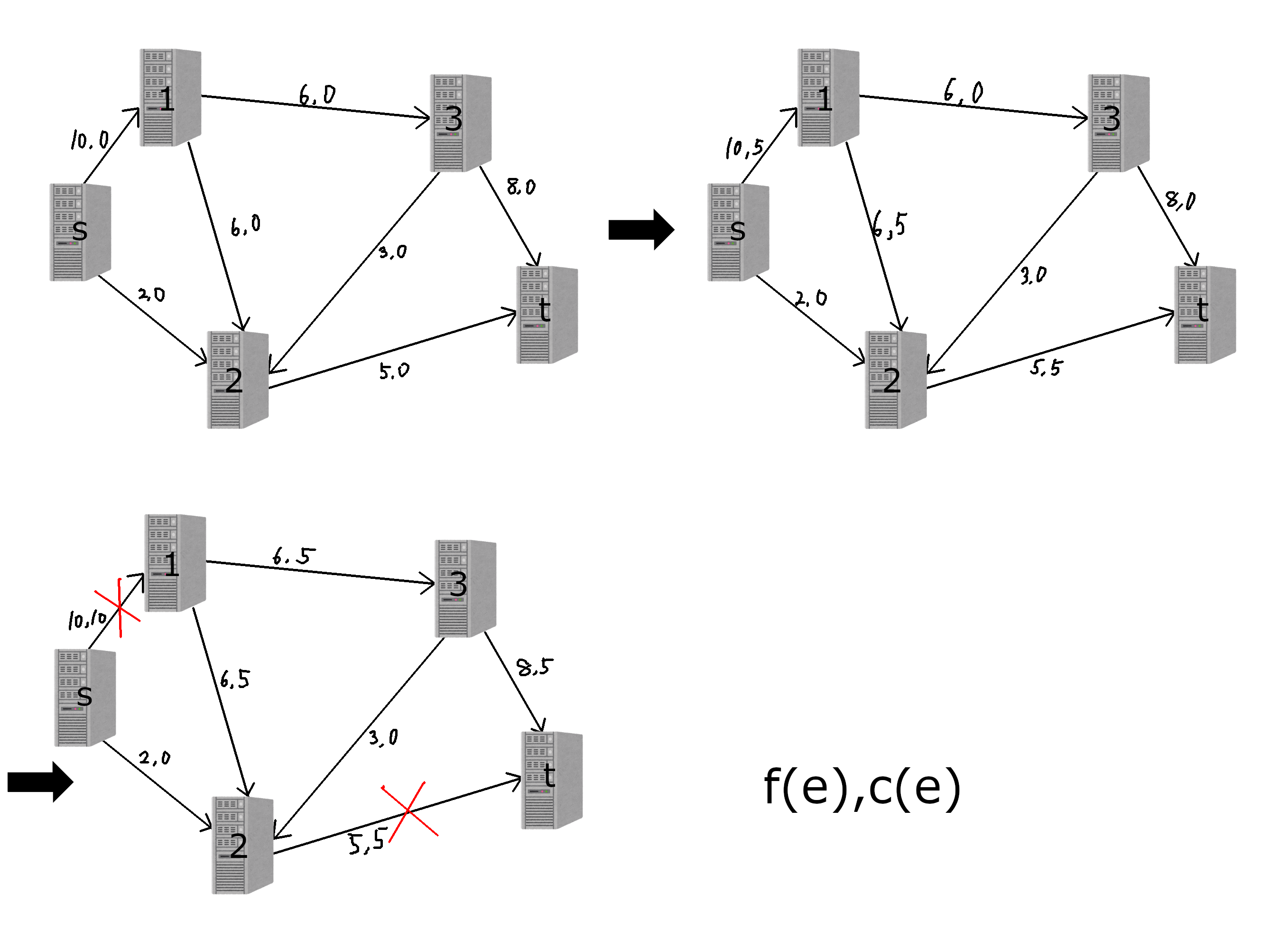
図: フロー...?
上に書いた貪欲に従って(s-1-2-t)に5,(s-1-3-t)に5で合計10流してみました。これで最大でしょうか...?実は最大ではありません。もっといい流し方があります。下に実例を挙げます。
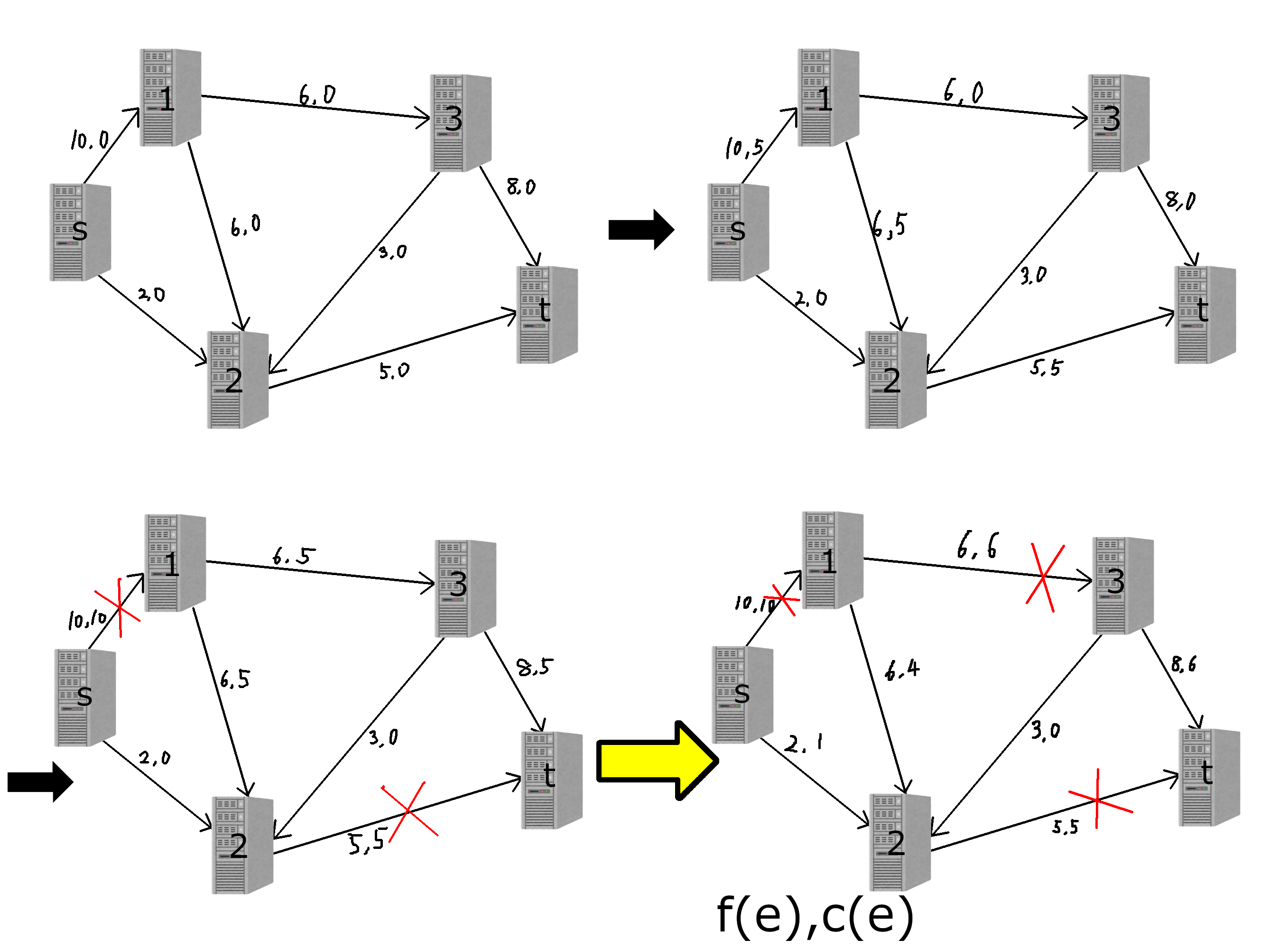
図: フロー
これで流量が11になり、最大です。この結果を得るためには先程の貪欲法に少し改良を加える必要があります。
- f(e)<c(e)であるeと、f(e)>0であるeの逆辺rev(e)のみを用いたsからtへのパスを見つける
- そのようなパスが存在しなければ終了。パスが存在したら、そのパスに沿って目一杯流して1に戻る(逆辺は逆向きに流すのでf(e)が減る)
この貪欲法で最大流量を求めることが出来ます。ここでは厳密な証明はしませんが、最小カットという概念を持ち出すことで証明できます。この方法はFord-Fulkerson法と呼ばれています。計算量は最大流をFとしてO(FE)です。こう書くと計算量は多そうですが、実際には深さ優先探索を行う回数がFになることはまず無いためもっと少ない時間で計算ができます。
実装
蟻本の実装を写経します...。今回はc(e)を変化させることで流量を反映させます。
Ford_Fulkerson.cpp
struct edge { int to,cap,rev; }; //MAX_Vは頂点数 vector<edge> G(MAX_V); bool used[MAX_V];//使用済みフラグ void add_edge(int from, int to, int cap) { //こう書くことでeの逆辺がG[e.to][e.rev]になる G[from].push_back({to, cap, G[to].size()}); G[to].push_back({from, 0, G[from].size() - 1}); } int dfs(int v, int t, int f) { if (v == t) return f; used[v] = true; for (int i = 0; i < G[v].size(); i++) { //次に考える辺 edge &e = G[v][i]; //使用済みでないかつキャパがある if (!used[e.to] && e.cap > 0) { int d = dfs(e.to, t, min(f, e.cap)); //もし流せるなら if (d > 0) { //流して e.cap -= d; //逆辺の許容量が増える G[e.to][e.rev].cap += d; return d; } } } return 0; } int max_flow(int s, int t) { int flow = 0; for (;;) { //使用済みフラグの初期化 memset(used, 0, sizeof(used)); //どれだけ流せるか int f = dfs(s, t, INF); //流せなくなったらその時点での流量の和を返す if (f == 0) return flow; //各回で流せた量をflowに足す flow += f; } }
フローにはまだまだ色々なテクニックや話題があるのですが、この記事では取り上げません。マッチング、最小費流問題などがあります。
11.6 他の話題
問題をうまく変形してノードを2色に塗り分けて考える問題や、木の上でDP(動的計画法)を行う問題などがありますが、ここでは解説しません。
11.7 まとめ
そろそろ文化祭前日ということで締切が近づいてきたので執筆を切り上げます。今回取り上げた内容は極めて入門的な内容ですので、競プロを始めてすぐの人の勉強になるかもしれませんし、ならないかもしれません。この記事を読んで競技プログラミングを始めたいと思った方は是非AtCoderやCodeforcesなどに登録してみて下さい。毎週のように刺激的で楽しい問題が出題されます。あと、蟻本を買うといいと思います。この本は本当に詳しくわかりやすく色々な事柄がまとめられています。
これからも精進を続けていこうと思います。皆さんは僕みたいに計画性の無い生活を送らないように、しようね!
拙い文章にお付き合いいただきありがとうございました。